Intermath: Investigations: Geometry: Triangles
If you double the lengths of each of the sides of a triangle, what happens to the perimeter and the area? Explain why.
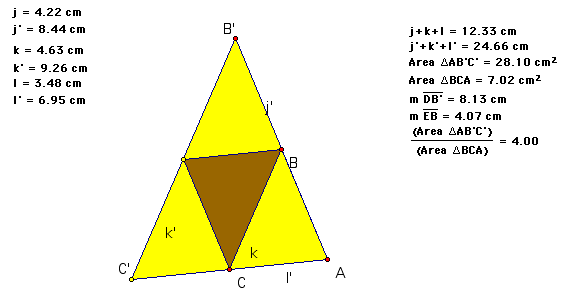
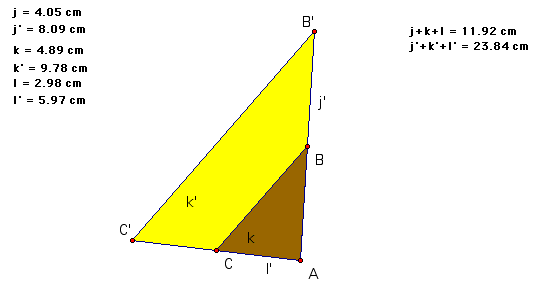
(This will be demonstrated with GSP sketches. The bright yellow triangle has sides twice the length of the gold triangle.)
From examining the sketch below notice that as the lengths of the sides double the perimeter also doubles. This only makes sense because the perimeter is simply the combination of the lengths of the sides, so obviously if what is being combined doubles, then the total length will also double.

The area is more interesting. Note on the sketch below that the heigths of the triangles have been added, remember that the area formula for a triangle is 1/2 the heigth multiplied by the length. As you can see from the measurement of these lines that the triangle with double the sides also has heigth that is doubled. Considering the measurements that go into our equation, area=1/2 base x heigth, the base of the doubled triangle is going to be doubled (x2) as is the height (x2). So we can conclude that the area of the triangle taking both those into account is going to be 4 times as large as the smaller triangle.
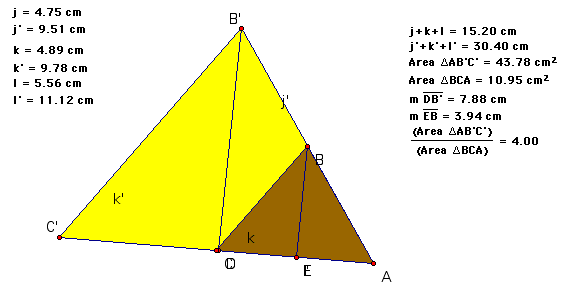
As you can see this has also been given as the ratio of the larger triangle over the smaller triangle. As the points are moved the ratio between the areas is consistently four. Look at another representation of the same idea below. There are four of the original triangle inside the triangle with double the area.