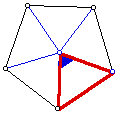
Intermath: Investigations: Geometry: Polygons
Find the measure of the vertex (blue) angle
of the red isosceles triangle that can be used to rotate the triangle
about its vertex to create a regular pentagon. What should the
measure of the vertex angle be if you want to create a square,
a regular hexagon, or
a regular n-sided polygon?

To best understand this, look at the sketch below.
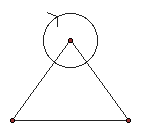
This shows that the interior angles as they travel around a vertex, of any four or more sided figure, will total 360 degrees - the same as the circle shown. Look at the sketch below to see if it is helpful in understanding. See how the vertex angle of each triangle creates the total degrees in the circle, so the combination of all the vertex angles must be 360. Then, if there are five triangles - each with a vertex angle - then the measure of each vertex angle is 1/5 of 360 degrees, or 72 degrees.
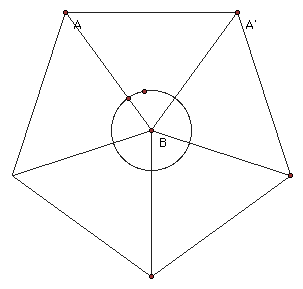
Another relationship that can be seen from this sketch and from others created is that the number of vertex angles is the same as the number of sides. For instance, look at the pentagon above. There are five vertex angles and there are also five sides that make the exterior of the polygon.
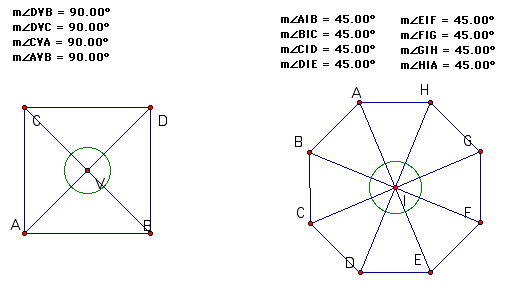
So when thinking about the second question, what would the vertex angle measure be for a square or hexagon. We can base our answer on the number of sides the shape has. A square has 4 sides, and therefore, has 4 vertex angles. The total measure of those angles will still be 360 degress, but the measure of one angle will be 1/4 of 360 degrees, or 90 degrees. The same can be done for a hexagon (an eight sided figure). The measure of one vertex angle is 1/8 of 360 degrees, or 45 degrees.
Lets look at those examples for fun, anyway.
Will any measure for this vertex angle in the
isosceles triangle create a regular polygon?
Explain why or why not.
Lets think about what we learned from the exploration above. The number of degrees in a circle - 360- divided by the number of sides the figure gives the measure of one interior vertex angle. So if we think about this backwards, we can better understand the answer to the question above. The measure of one of the vertex angles is equal to 360 divided by the number of exterior sides of the figure. Or what numbers for the measure of the vertex will produce any number of exterior sides. Well, now we have to consider a few things. What we have learned is only true for figures that have four or more sides. Additionally, regular polygons all have the same side lengths, therefore the number of exterior sides must be a whole number. If it were a rational number, then the number of exterior sides would not create a closed figure, which is a requirement for a regular polygon. So NO, not any measure for a vertex angle creates a regular polygon. Only those measures that give whole numbers, four or more, when they divide 360 degrees.