
By Angel Abney, Andy Tyminski, and
Pawel Nazarewicz
Mathematics is all around us. As we discover more and more
about our environment and our surroundings we see that nature
can be described mathematically. The beauty of a flower, the majesty
of a tree, even the rocks upon which we walk can exhibit nature's
sense of symmetry. Although there are other examples to be found
in crystallography or even at a microscopic level of nature, we
have chosen representations within objects in our field of view
that exhibit many different types of symmetry.
This semester in transformational geometry has altered our
views, or at least our viewfinders. It seems that everywhere we
look now our eyes are drawn first to the patterns of symmetry
that exist, and that the object itself is a secondary consideration.
So, come join us as we examine examples of bilateral symmetry,
radial symmetry, strip patterns and wallpaper patterns in nature.
You'll never look at your world the same way again...
|
Begin
your exploration here ...
Click on any of the topics below to explore how
that symmetry type can be found in nature:
|
| |
 |
|
Radial symmetry is rotational symmetry around a fixed point
known as the center. Radial symmetry can be classified as either
cyclic or dihedral.
Cyclic symmetries are represented with the notation Cn, where
n is the number of rotations. Each rotation will have an angle
of 360/n. For example, an object having C3 symmetry would have
three rotations of 120 degrees.
Dihedral symmetries differ from cyclic ones in that they have
reflection symmetries in addition to rotational symmetry. Dihedral
symmetries are represented with the notation Dn where n represents
the number of rotations, as well as the number of reflection
mirrors present. Each rotation angle will be equal to 360/n degrees
and the angle between each mirror will be 180/n degrees. An object
with D4 symmetry would have four rotations, each of 90 degrees,
and four reflection mirrors, with each angle between them being
45 degrees.
|
 |
 |
 |
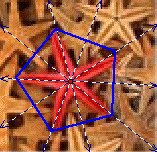
| A starfish provides
us with a Dihedral 5 symmetry. Not only do we have five rotations
of 72 degrees each, but we also have five lines of reflection. |
Another example of a
starfish - as we can see, starfish can be embeded in a pentagon,
which can then be connected to the Golden Ratio ... |
Also found in the sea
are sand dollars. They too, have D5 symmetry. |
 |
 |
 |
| Jellyfish have D4 symmetry - four rotations of
90 degrees each. It also has four lines of symmetry, and in the
middle you have a four-leafed clover for good luck. |
Flowers offer a variety of radial
symmetry. |
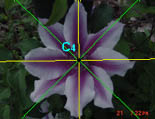
Hibiscus - C5 symmetry. The petals
overlap, so the symmetry might not be readily seen. It will be
upon closer examination though. |
 |
 |
 |
| This hibiscus is slowly wilting
away, and the C5 symmetry is really evident. |
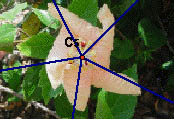
After some debate, we decided that
this flower has C4 symmetry - one row of the petals is underneath
another. |
Petunias offer some patriotic D5
symmetry. |
Go back to the top menu.
 |
|
Strip pattern symmetry can be classified in seven distinct
patterns. Each pattern contains all or some of the following
types of symmetry: Translation symmetry, Horizontal
mirror symmetry, Vertical mirror symmetry, Rotational
symmetry, or Glide reflection symmetry.
The seven types are T, TR, TV, TG, TRVG, TGH, and TRGHV.
|
 |
 |
 |
| An Eastern White Pine
has interesting symmetry on it's trunk. Each year, as the tree
grows, it develops a new ring of branches (most of which have
been broken off in the picture above). The rings move up by similiar
translation vectors, but some variation occurs due to the conditions
for that year. |
Another picture of the
white pine - this time with branches showing. The white pine
exhibits T symmetry. |
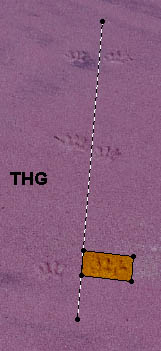
Here is a set of animal
tracks that exhibits THG symmetry. Because we have a horizontal
mirror, we get a glide by default. I think that these are armadillo
tracks. |
 |
 |
| Here are some footprints on the beach -
in them, we can see a translation and nothing else. That pattern
is a typical T. I'm not sure how this pattern was accompished,
but it looks like whoever did it had two left feet ... |
Here is a set of radioactive footprints
creating a TG pattern. John Conway simply calls this "step". |
 |
 |
|
The copperhead is one of the four poisonous snakes in
the United States. Can you name the other three? Highlight the
text between the arrows for the answer:
>> The Cottonmouth (Water Mocassin),
Rattle Snake, Coral Snake <<
As with most snakes, it has TRGHV symmetry.
|
The black rat snake is a non-poisonous snake,
and like the copperhead (and most other snakes with patterns),
it has TRGHV symmetry. |
 |
| In the process of working with strip patterns,
we have discovered that in fact, there is an eighth symmetry
- the delightful MRT symmetry. Ha ha ha! No really ...
I pity the fool who don't tesselate the plane ... |
Go back to the top menu.
 |
| Wallpaper patterns are patterns of symmetry
that tessellate the plane from a given fundamental region. There
are seventeen different types of wallpaper patterns. In the examples
below, you will see the fundamental regions highlighted, as well
as the translation vector generators that can be used to complete
the pattern by translation, after the other isometries of the
pattern are completed. |
 |
 |
| The Giant's
Causeway, located in Ireland, is an fascinating *632 formation
found in nature. It is a collection of hexagons tesselating the
ground - even in 3D at some points. |
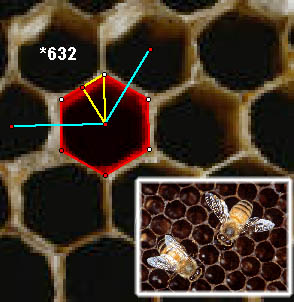
Bees form their honeycombs in a
*632 pattern as well. There seems to be a lot of hexagonal symmetry
in nature. Any conjectures on why that's the case? The answer
lies with steiner
points and minimal networks. |
Go back to the top menu.
 |
|
Bilateral symmetry is symmetry across a line of reflection.
Are people symmetric? We think we are, but upon closer analysis,
we are less symmetric than we think. The more simple the creature
(ants --> elephants), the more likeley it is that it will
be perfectly symmetric.
We took two professors, cut and pasted half of their head
in Photoshop, and flipped that half horizontally. We then aligned
the two halves so that it came closest ro resembling a human
head. You be the judge on how good of a job we did and how symmetric
people around us are in general ...
|
 |
 |
 |
| Here is our professor - Dr. Clint
McCrory, who as you will see, is very symmetrical. |
Which side of Dr. McCrory do you
think this is ... ? |
... and this one? How quickly did
you pick up on the differences? |
 |
 |
 |
| Dr. Larry Hatfield has a part on
the side of his head which makes it easier to notice the symmetry
involved. |
Here we can see his right side of
the face reflected over the middle ... |
... and the left side. As you can
see, one is more predominate than the other. What are some things
that would contribute to this asymetry? |
Go back to the top menu.
Want to learn more?
Here are a few links of interest:
-- Symmetry in crystals
and how it effects light.
-- Our Math 5210/7210 class
page - there are tons of links on that site as well.
-- If you need any of the terms on this webpage defined, you
can check out Intermath
- a project that's being worked on here at UGA. If Intermath doesn't
have what you need, you can always check out Mathworld.









