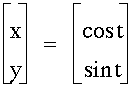
1.
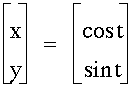
2. 
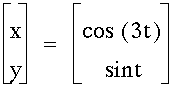
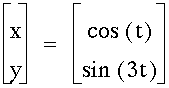
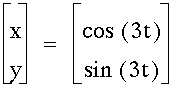
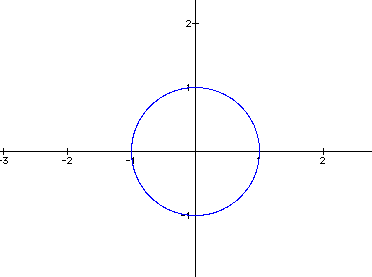
My conjecture is: As long as a and b are the same, the two parametric equations represent a circle.
This is not true, as follows:
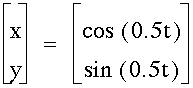
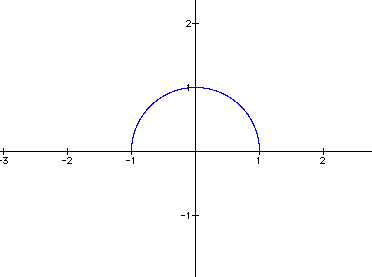
However, if t has domain 0.....12.56, we can get the entire circle again.
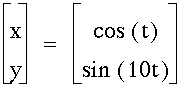
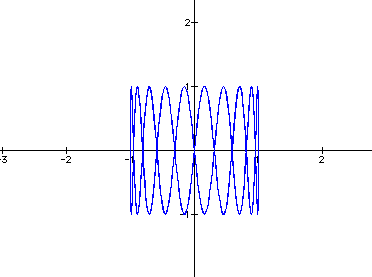
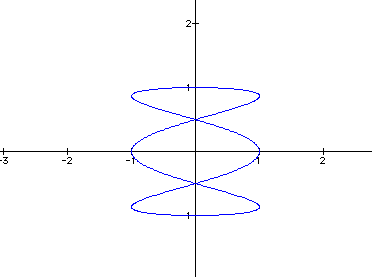
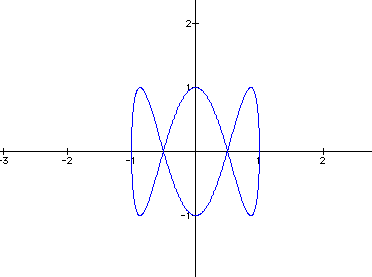
It appears that the value for b corresponds to the number of loops in the figure.
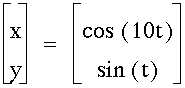
Here, there are 10 vertical loops.
3. 
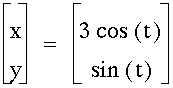
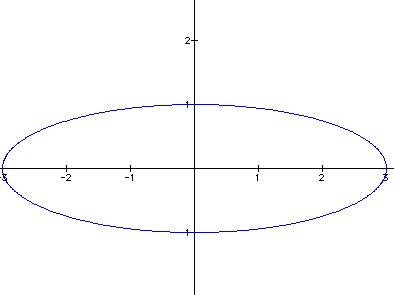
Varying a and b changes the distance from the origin on the x and y axis, respectively.
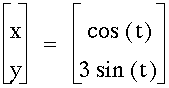
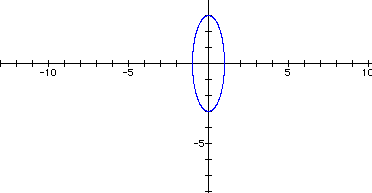
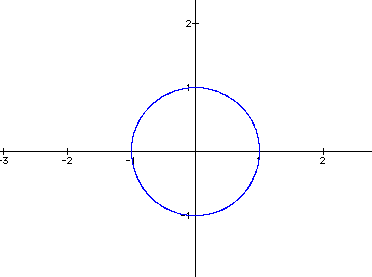
If a and b are the same then we have a circle of radius a=b.
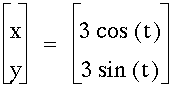
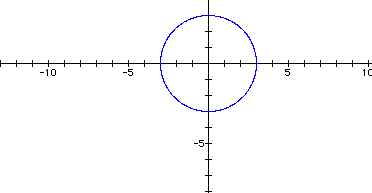
4. 
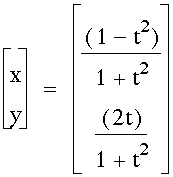
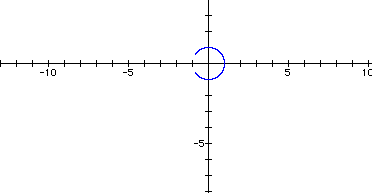
The circle is not complete. I am going to vary the values of t and attempt to draw the entire circle.
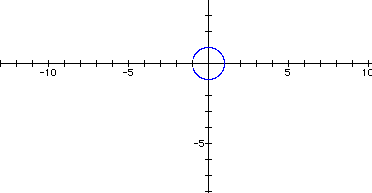
Here the values of t are between and including -6.28 through 6.28.
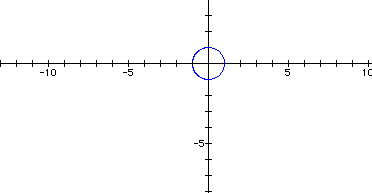
Here the values of t are between and including -12.56 and 12.56 or 4 pi.
5. The following are graphs of
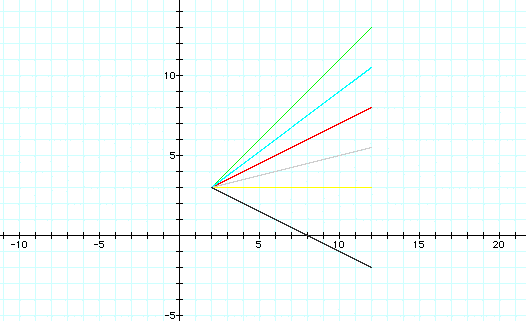
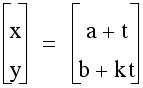with a =2, b=3 and different values
of k. We notice that while all line segments begin at the point
(2,3) and end with the (x,y) with based on t =10, however the
lengths of the segments are different. The longest segment is
the with value k=1 and the shortest segement has k value as 0
and then .25. One question that can be asked is what makes the
segment lengths different?
In question #3 on this assignment, we looked at creating a circle with parametric equations using x=acos t and y = bsin t , with a and b the same. This circlewas centered at (0,0). Now, we look at parametric equations using sin and cos that create a circle not centered at (0,0).
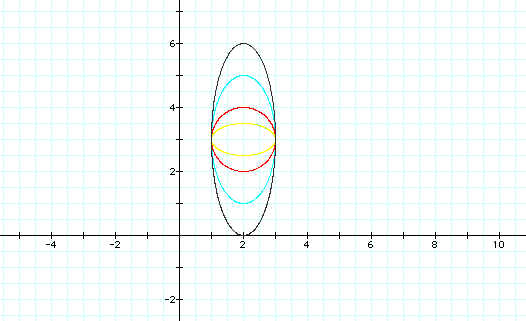
The red circle is the graph of x = cos t and y = sin t. The ellipses are graphs of variations on k in
.
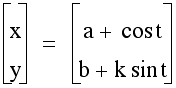