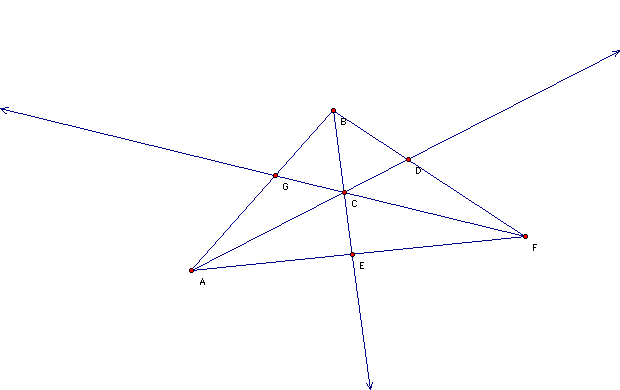
Using Geometer's Sketchpad, we can look at an example of the conjecture:
The three angle bisectors of the internal angles of a triangle are concurrent.
Example: 
The angle bisectors are: AD, BE and FG. They are concurrent because the point c is on all of the angle bisectors. Each angle bisector divides the opposite side into two segments.
Proof:
For triangle ABC, first we construct the angle bisectors of <ABC and <ACB. They intersect at the point l.
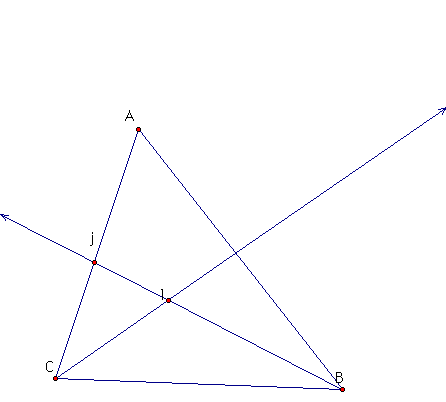
Now construct perpendicular lines from l to AC, from l to AB, and from l to BC.
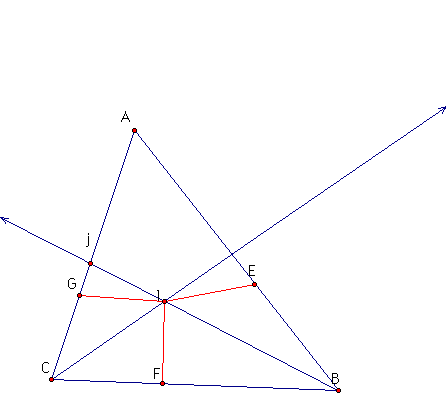
Triangle GlC is congruent to triangle FlC by ASA. This gives us that lG = lF.
Triangle ElB is congruent to triangle FlB by ASA. This gives us that lE = lF.
So we have, lG = lE = lF. Construct a line from A to l.
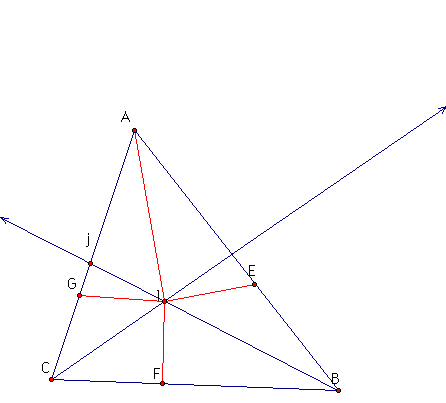
Triangle AGl and triangle AEl are both right triangles. The two triangles are congruent because the hypoteneuse and the adjacent leg are equal. Therefore <GAl = < EAl, such that Al is the angle bisector. It is concurrent with the other two at the point l.