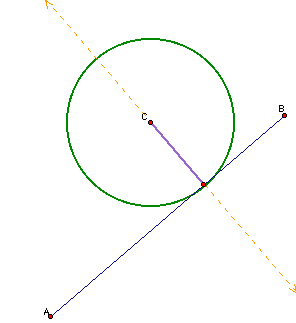
Lets begin by looking at circles tangent to a line. We can use the following construction, to do this:
1. draw a line segment AB,
2. pick a point in the plane, not on segment AB, call it C because it will be the center of our tangent circle.
3. Drop a perpindicular from point C to the AB segment.
4. The segment from point P perpindicular to AB, will be the radius.
5. Now, construct the circle.

script tool for this construction
Next, lets try to draw a circle tangent to another circle.
We can do this by drawing one circle and picking a point on the original circle, and picking a point in the plane to be the center of the tangent circle. We connect the center of the original circle and the point we in the plane with a segment. The point in which the segment intersects the original circle will be point of tangency. We can construct our tangent circle using the center and the point of tangency.
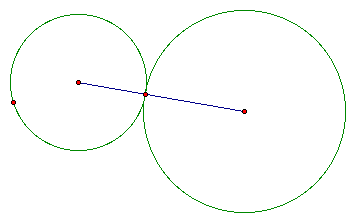
sript tool for two tangent circles
Given two circles, lets explore finding a third circle tangent to the other two.
The construction is as follows:
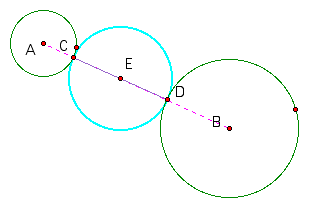
Start with two non-adjacent circles. Call their centers A and B. Construct segment AB.
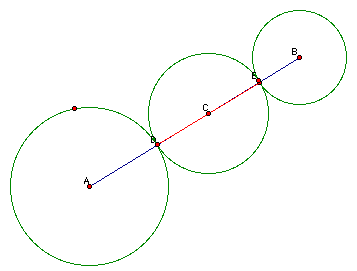
Label the intersection of AB with the two circles, C and D and construct segment CD. Find the midpoint of CD and label it E.
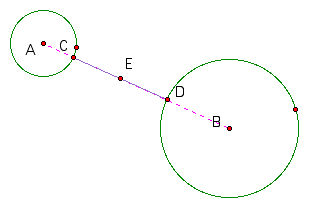
Construct a third circle with E as the center and ED as the radius. This circle is tangent to the other two.
script tool for three tangent circles
For the next exploration, lets figure out how to take two circles, one inside the other and find a circle tangent to both circles.
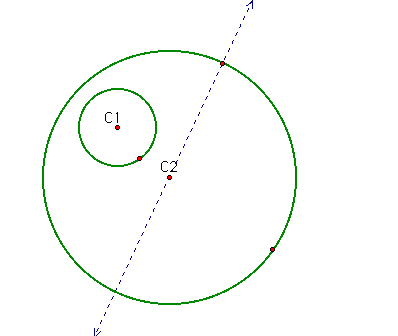
First start with two circles, one completely inside the other.

Through the chosen point of tangency on the bigger circle, construct a line connecting the chosen tangent point and the center of the bigger circle.
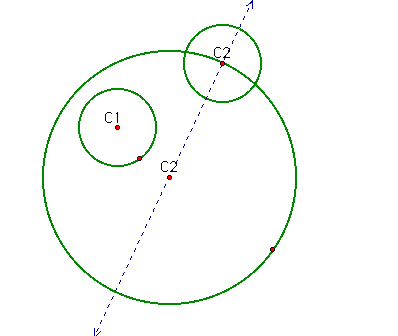
Next construct a copy of the smaller circle with center the chosen point of tangency on the larger circle.
Construct the outermost intersection of the original line through C2 with the constructed circle. Connect the intersection with C1, the center of the smaller circle. Find the perpindicular bisector of the segment. The point where the perpindicular bisector and the original line intersect will be the center of our tangent circle.
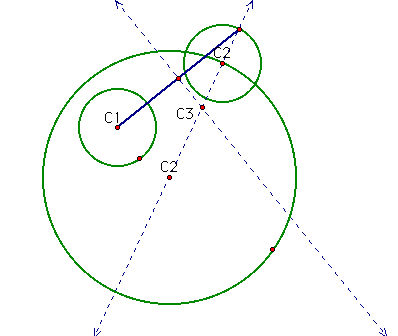
Now construct the isoceles triangle. This triangle will always be isoceles.
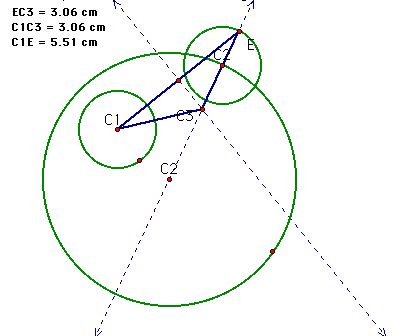
Using C3 as the center and the segment C3C2 as the radius, construct the tangent circle.
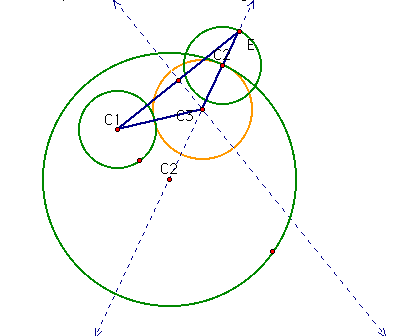
Script tool to make tangent circle