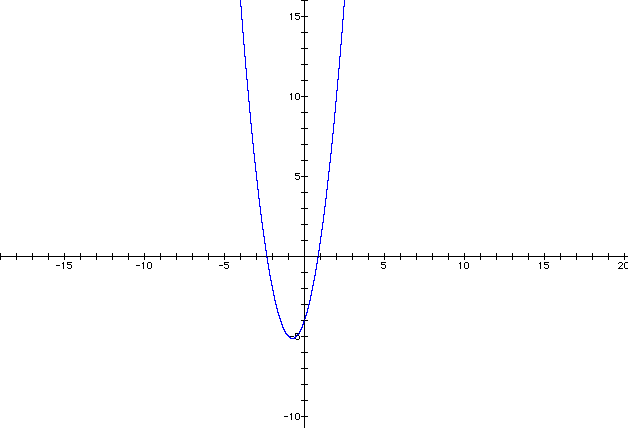
6. Graph y=2x^2+3x-4
i. Overlay a new graph replacing each x by (x - 4).
ii. Change the equation to move the graph into the second quadrant.
iii. Change the equation to produce a graph concave down that shares the same vertex.
This is the
graph of the equation 
.
If we replace x with (x-4) , we get the following graph:
in blue, and
in red
The original graph has been shifted to the right 4 units. We can be sure of this because the vertex of the original graph in blue is (-.75, -5.125) and the vertex of the tranlated graph in red is (3.25, -5.125). The y-value has not changed, but the x-value is four more than the x-value of the original graph.
To move the graph into the 2nd quadrant, we must move the graph to the left. When we replaced x with (x-4), the graph was translated to the right 4 units, so to move it to the left, we should replace x with x+c, where c is a positive value.
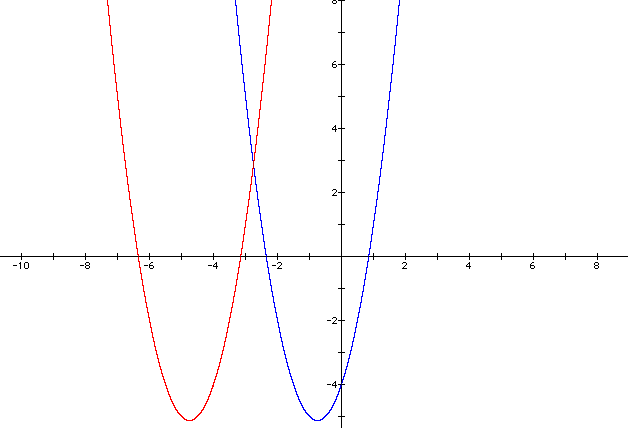
in blue
in red
We have moved the graph to the second quadrant, but note the entire parabola does not lie in the second quadrant. It is partially in the third and if we trace the parabola it is in the first quadrant eventually, as well.
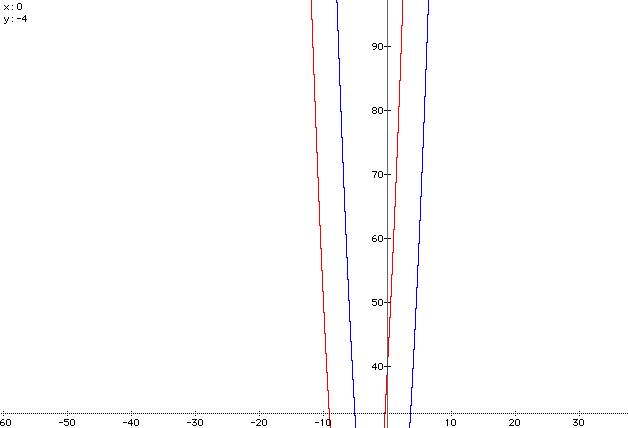
Here the parablola intersects the y-axis at its y-intercept .
The last task
is to find a parabola that is concave down with the same vertex
as our original parabola. We have found that the vertex of the
original parabola is (-.75, -5.125). We also know that the equation
of a parabola can be written in the form 
,
where (h,k) is the vertex of the parabola. What we really want
is a reflection of the original graph about the x-axis. We can
make this happen by making a negative. The equation of the graph
that we want to find is,
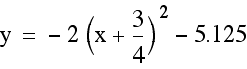in red,
.
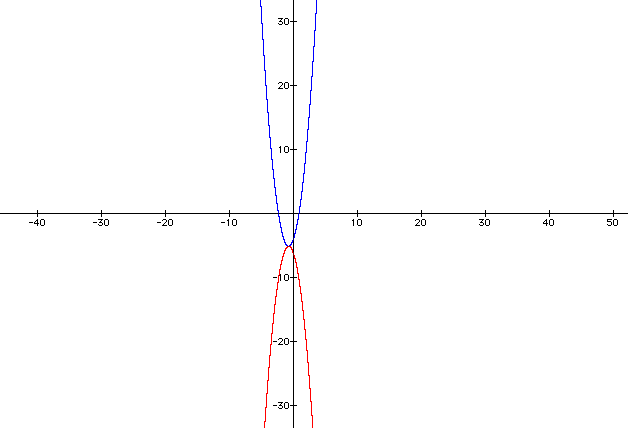