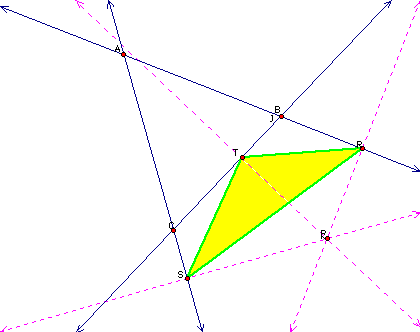
The following is a pedal triangle:

It is created by picking a point P anywhere in the plane and drawing a triangle ABC anywhere in the plane. Next, we draw perpindicular lines from P to the sides of the triangle, ABC. Connecting the points where the perpindicular lines intersect the triangle, we form our pedal triangle.
Exploration #1:
Suppose point P is the centroid of the triangle. Then the pedal triangle is circumscribed in the original triangle.
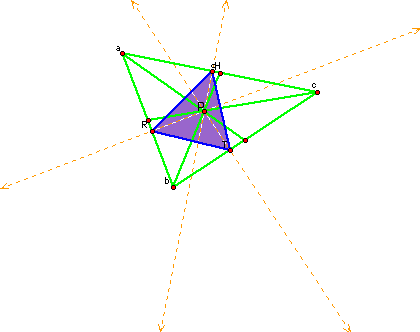
Exploration #2
What if P is the incenter?
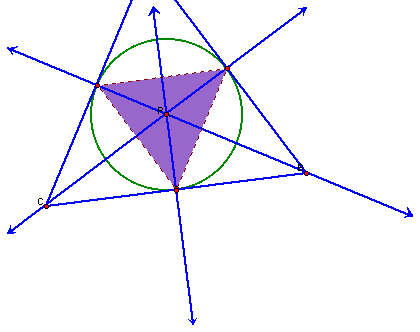
Exploration #3
What if P is the orthocenter?
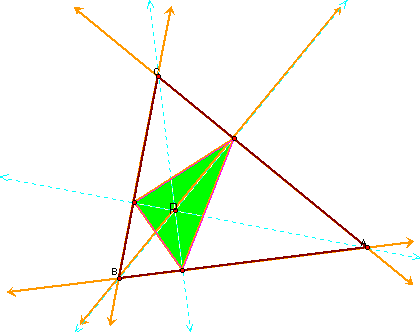
If the orthocenter is outside the triangle....
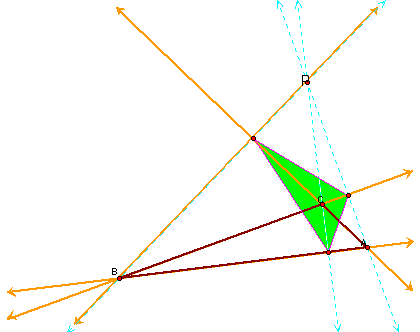
Exploration #4
What if P is the circumcenter?
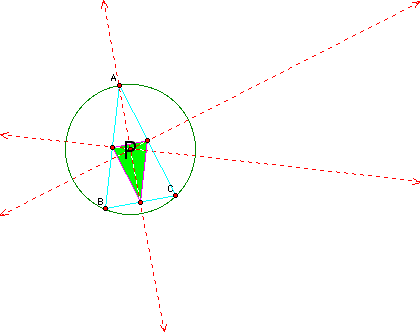
Exploration #5
What if P is one of the vertices of the triangle ABC?
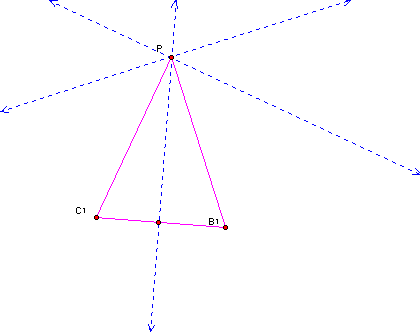
When P is one of the vertices of triangle ABC, we cannot draw the pedal triangle because there will be only two distinct points of intersection.
Exploration # 6 - What if P is one of the vertices on triangle ABC?
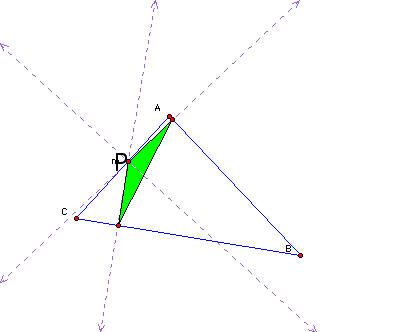
Exploration #7 - Find all conditions in which the three vertices of the Pedal triangle are colinear.
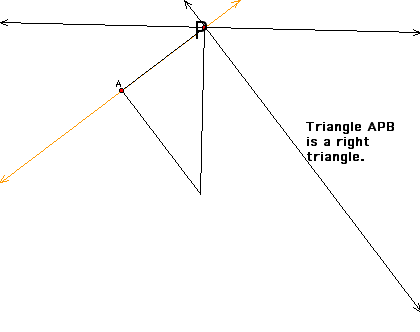
The case where the triangle is a right triangle and P is the shown vertex gives the case where the intersection is one point. The Pedal triangle cannot be made.