Complete a Write-up on your Web Page for the following investigation. This should be individual work.
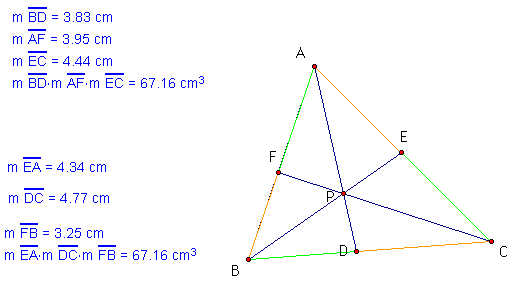
A. Consider any triangle
ABC. Select a point P inside the triangle and draw lines AP, BP,
and CP extended to their intersections with the opposite sides
in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

(AF)(BD)(EC) = (FB)(DC)(EA), regardless of where the point P is placed. My hypothesis is that this is true because of some ratio of the corresponding sides of the triangle ABC.
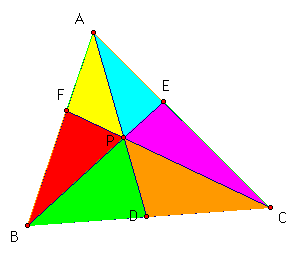
Using the various
line segments through the point P, there are 6 different triangles
to look at. We can assume that several are similar which supports
that a common ratio of the sides, may exist. Using parallel lines,
we can find the following two similar triangles: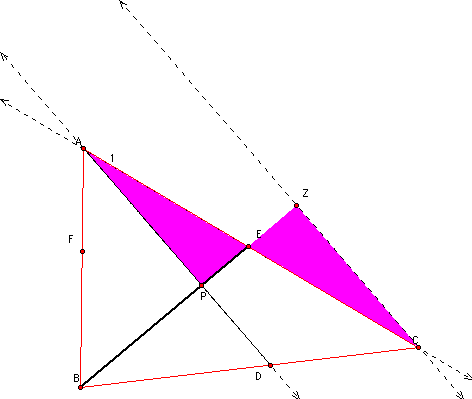
Based on the parallel lines shown, the following pairs of angles are equal. <ZEC = <PEA and <ZCE = <EAP. Therefore, the two shaded triangles must be similar which implies that AP/CZ = AE/EC. Again, using parallel lines, we can show that the following two shaded triangles are parallel, as well. <AFP = <XFB, and <FBX = <FAP, such that the following proportion is true, AF/BF = AP/XB.
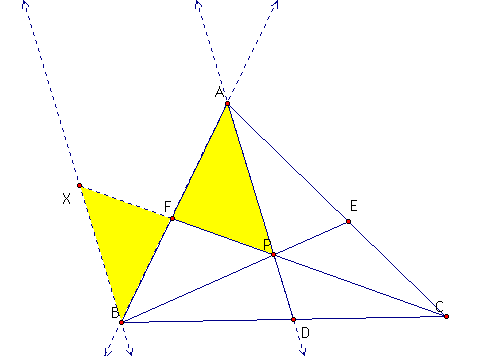
Because of corresponding angles and the common angle, the following two shaded triangles are similar:
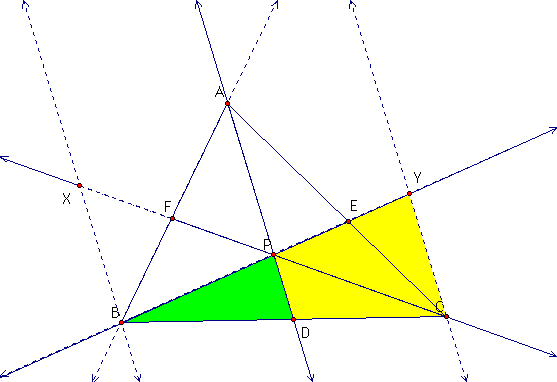
and the following two triangles are similar for the same reason.
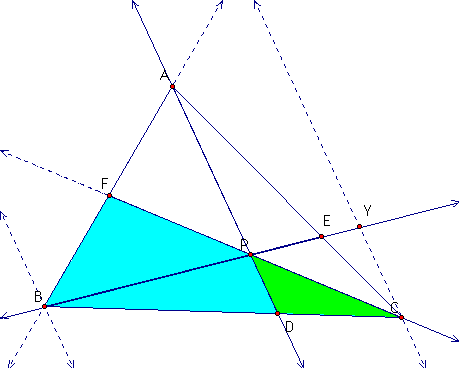
Such that we get the following proportion based on Ceva's Theorem:
AF/BF * BC/CD * CD/BC * CE/AE =
AP/BX * DP/CY * BX/DP * CY/AP.
We can simplify this and get the desired result, (AF)(BD)(EC)/(FB)(DC)(EA) = 1.
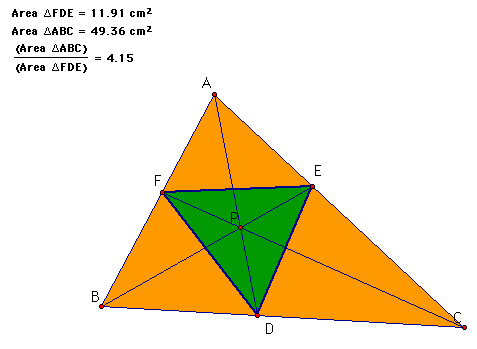
The ratio of the areas of the two triangles will always be greater than or equal to 4. To see this click here.
When will the ratio be exactly 4? Here are some ideas that I tried:
P is the orthocenter (didn't work).
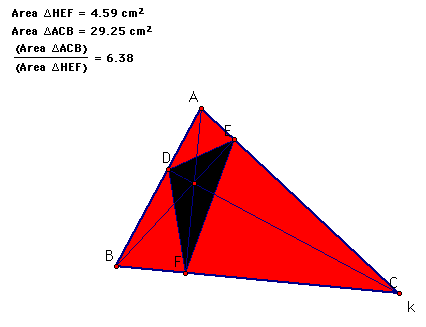
P as the incenter, does work.
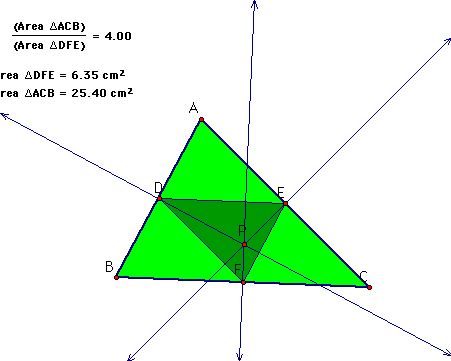 .
.