The purpose of this assignment is to investigate tangent circles. The problem:
Given two circles and a point on one of the circles. Find a circle that is tangent to both circles with one point of tangency being the designated point.
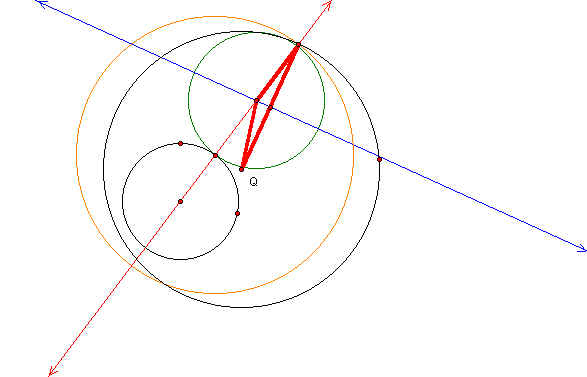
There are several cases that need to be considered. First the case is when one circle is inside the other and the designated point is on the smaller circle. Using the following construction the tangent circle was found. The given circles are black and the tangent circle is green. The red isosceles triangle and the blue perpendicular bisector of the base were used to constant the tangent circle.

When the movement of the designated point on the smaller circle is examined we can see that the sum of the segments from the center of the given circles to the center of the tangent circle is constant. Therefore the locus of the centers of the tangent circle is an ellipse and the foci is the centers of the given circles. By tracing the perpendicular bisector (at the center of the tangent circle) of the base of the isosceles triangle the envelope is constructed. Click here to see the animation of the following sketch in GSP.
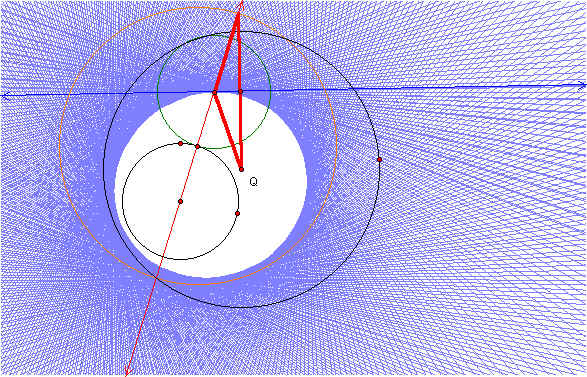
The second case to be considered is when the smaller circle is outside of the larger circle. For this case the same construction can be used. When the designated point on the smaller circle is animated and the perpendicular bisector is traced, the loci and envelope created is a hyperbola. Here the difference of segments AB and AC is constant. This is represented in the following sketch where the two black circles are the given circles and the green circle is the tangent circle. Click here to see the animation in GSP.
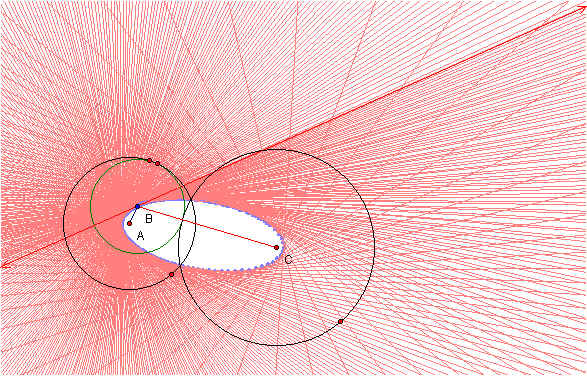
The third case to consider is when the the circles intersect each other. Here again we use the same construction. When the designated point of tangency is animated and the locus is traced we obtain an ellipse. Again the sum of the distance of AB and BC is constant. The sketch below shows the ellipse and envelope resulting from the animation. Click here to see the animation in GSP.
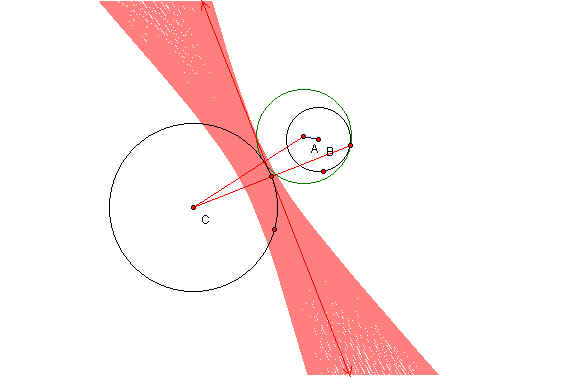
The last case to consider is when the circles are tangential to each other. This is shown in the following sketch.
In this case the loci is two parabolas where the difference between the distance of the centers of the given circles and the tangent circle, AB and AC, is constant. The following sketch shows the construction of the parabolas when the loci and perpendicular bisector of the isosceles triangle is traced. Click here to see the animation in GSP.
