EMAT 6700- Instructional Unit

Geometry

Objective: To enhance student learning through interactive lesson plans using technology. To have students produce geometric formulas using technology. To have students generate concurrencies using technology. To further advance students knowledge of Geometer’s Sketchpad.

Prerequisites: Students do not need to be familiar with Geometer’s Sketchpad. They should understand and be familiar with the definitions of shapes such as triangles, circles, and rectangles before beginning this lesson. The entire lesson plan requires a computer lab setting.

Lesson Plan:

In this first section students produce the equation of a circle by exploring circles in Geometer’s Sketchpad. Students are asked to follow these directions as they explore.

1. Under Graph choose Show Grid.
2. Under Edit set the preferences to centimeters for distance, degrees for angles and tenths for precision.
3. Use the circle tool and make at least 5 different circles, varying the size of each.
4. Under the Graph menu choose the snap to grid option.
5. Move the center of each circle to a lattice point. Move the defining point of each circle to a lattice point.
6. Select each circle and under the construct menu select circle interior to construct it. While the interior is selected, choose a color from the display menu. Make each circle a different color.
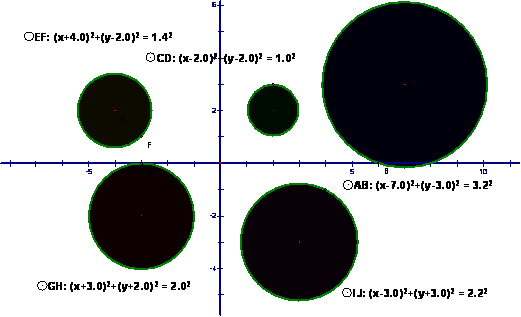
7. Make a record of your constructions: See figure 1 below for example.

Color of Circle	Center of Circle	Radius
RED	-3,-2	2
BLUE	7,3	√10
GREEN	2,2	1
YELLOW	-4,2	√2
PURPLE	3,-3	2

8. Select each circle without selecting its area. Under Measure select Circumference then Area.
9. Is there a relationship between the center and the radius of the circle and its circumference and area? Explore to check your conjecture.

Appropriate amount of time is given here for students to explore this relationship.

10. Select one circle. Under Measure select Equation. Was your conjecture correct? If not why?
11. Explain how the center and the radius are incorporated into the equation.
12. Produce the correct equations for all the circles and move each equation by its corresponding circle.
13. Write the equation for a circle with center (-1, 5) and radius = 3. Now create one such circle in GSP and check yourself using the measure tool.
14. Now using the select tool, move the equations to the upper right corner of your screen.
15. Switch computer stations and match the equations to the circles. Explain how you know your equations are on the right circles.

In the second section students generate shapes in GSP. As an introduction students would construct a rectangle in order to learn how to construct perpendicular and parallel lines.

Constructing a rectangle:

1. Using the segment tool draw a segment of any size.
2. Then select a point on the segment and the segment itself. Under the construct menu choose perpendicular line.
3. Then select the other point on the original segment and repeat the perpendicular line construction.
4. Determine the length of the side by constructing a point on one of the perpendicular lines.
5. Select this point and the line it is on and construct another perpendicular line.
6. Select the two intersecting lines and under the construct menu choose intersection. (NOTE: You may be able to simply click on the intersection to construct a point there.)
7. Why is this a rectangle? What are its properties? Click and drag one of its vertices. Does it remain a rectangle?
8. How would you construct a square? A triangle? An equilateral triangle? Click on one of the vertices and drag your shape to see if your construction is correct and the shape remains.

Here again students are given the opportunity to explore and construct shapes. They are encouraged to work with others. Eventually the option of rotation under the transformation menu is introduced. Also if the idea of creating these shapes within a coordinate system is suggested students need to understand its limitations. You cannot drag only one point in order for the shape to remain a square.

9. Construct a segment using the segment tool. Double click on one of the endpoint until you see it marked by a flash of concentric circles. Now select what you want to rotate. Under the transformation menu select the rotation option. Determine your angle of rotation and click OK.
10. You can continue to use rotate to construct your square.
11. If you used the coordinate system to construct your square, did your click and drag test work?

In the third section students generate concurrencies in GSP. Students would begin by exploring sets of lines in triangles.

1. Construct a triangle using the segment tool.
2. Construct the midpoints of these segments by selecting these segments and choosing midpoint under the construct menu.
3. Construct the perpendiculars to the sides of the triangles through these points.
4. What do you notice? Is it true for any triangle?
5. Draw a new triangle.
6. Construct the midpoints again. Construct the medians of the triangle (the segments that connect the midpoints with the vertices opposite the midpoints).
7. What do you notice? Is it true for any triangle?
8. Draw a new triangle.
9. Construct altitudes of the triangle (the lines perpendicular to the sides but that go through the vertex opposite that side).
10. What do you notice? Is it true for any triangle?
11. Draw a new triangle.
12. Construct the angle bisectors of the triangle.
13. What do you notice? Is it true for any triangle?

When three or more lines meet at a single point, they are said to be concurrent. The following facts are true for every triangle:

The medians are concurrent; they meet at a point called the centroid of the triangle. (This point is the center of mass for the triangle. If you cut a triangle out of a piece of paper and put your pencil point at the centroid, you would be able to balance the triangle there.)

The perpendicular bisectors are concurrent; they meet at the circumcenter of the triangle. (This point is the same distance from each of the three vertices of the triangles.)

The perpendicular bisectors are concurrent; they meet at the circumcenter of the triangle. (This point is the same distance from each of the three vertices of the triangles.)

The altitudes are concurrent; they meet at the orthocenter of the triangle.

The angle bisectors are concurrent; they meet at the incenter of the triangle. (This point is the same distance from each of the three sides of the triangles.)

Triangles are the only figures where all these concurrencies always hold.

Homework Problem: Recall that the centroid is the center of mass of a geometric figure. How could you construct the centroid of a square?

Solution: One can use a straightedge to construct the two diagonals of the square. The centroid is the point of their intersection. Or one can construct the perpendicular bisectors of two consecutive sides of the square. The intersection of these bisectors is the same centroid.

In this fourth section of the lesson plan students would be given an entire period to explore the following problem.

In Class Problem: Draw five quadrilaterals Use one quadrilateral for each construction below.

1. Construct the eight medians of the first quadrilateral. (There will be two medians at each vertex.)
2. Construct the four midlines of the second quadrilateral.
3. Construct the four angle bisectors of the third quadrilateral.
4. Construct the four perpendicular bisectors of the sides of the fourth quadrilateral.
5. Construct four altitudes in the fifth quadrilateral -- one from each vertex.

Do these constructions with a few different quadrilaterals. Don't use only cases like squares and rectangles. Record any observations about the constructions above. How is this different from what you saw with triangles?

Solution: For some quadrilaterals (specifically those which can be inscribed in a circle), the concurrency of perpendicular bisectors holds. For all quadrilaterals, the midlines come in pairs that are parallel. For some quadrilaterals (specifically those which can have a circle inscribed in them), the angle bisectors are concurrent.

In this fifth section students continue their exploration of triangle centers with the Nagel point and the Gergonne point.

1. Construct a triangle. Extend the segments of the triangle by constructing parallel lines.
2. Construct the circle tangent to one of the sides of the triangle and the line extensions of the other two sides. This circle is called the escribed circle. First construct the center of this circle. The center at the intersection of the exterior angle bisectors. For example in the following diagram the red circle is the escribed circle of triangle ABC whose center, D, is at the intersection of the angle bisectors of angles FCA and EAC.

3. Once the center is constructed, we need to construct the radius. How would you find the defining point of this circle?

Constructing a line through the center of the circle and perpendicular to any of the lines the circle will be tangent to will give us the defining point. Now that we have a center and a defining point we can construct the circle.

NOTE: The hide option under the Display menu can be used to unclutter the screen and hide any lines that may interfere with future constructions.

4. Repeat the escribed circle construction for all three sides of the triangle.
5. Construct a line through the center of the escribed circle and the point of tangency of the circle and triangle. What do you notice? Is it true for any triangle?

The point constructed is the Nagel point.

6. Construct a new triangle.
7. Construct the incenter.
8. Construct a circle with its center at the incenter and tangent to all three sides of the triangle. This circle is called the incircle of the triangle.

Again constructing a line through the center of the circle and perpendicular to any of the segments the circle will be tangent to will give us the defining point.

1. Now construct the segment from the point of tangency of the incircle and triangle to the opposite vertex. What do you see? Is it true for any triangle?

This point constructed is the Gergonne point.

Homework: Find at least one more triangle center or line and find how to construct it in class tomorrow. Be ready to present your find to the class.