EMAT 6690- Essay # 1
Trisecting the Area of a Triangle
Given any triangle ABC, we
can find a point D such that line segments AD, BD and CD trisect the area of
the triangle into three regions with equal areas.
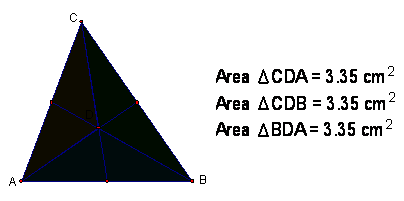
Since point D is the centroid
of triangle ABC, we can construct point D by constructing the medians of
triangle ABC. The intersection of the medians, or the point of concurrency, is
the centroid. Click here to see the
construction of the centroid in GSP.
We can prove that the
centroid trisects the area of triangle ABC into three regions of equal area.
First we need to trisect the area of one of the smaller triangle such as
triangle ADB. If we trisect the base of this triangle, AB, then we can trisect
the area of the triangle. We trisect the segment AB by creating the midpoint of
segment AD, point F.

Then we construct a line
parallel to AC through point B. We
construct points F’ and D’ on the parallel line through B on the opposite side
of AB from F and D such that AF = BF’ and AD = BD’. When we construct segments
FF’ and DD’ we obtain the intersection of these segments and segment AB, points
H and G, respectively. These points trisect segment AB into equal segments. Click here to see this
construction in GSP. If we connect
points H and G to vertex D we obtain the trisection of the area of triangle
ABD.
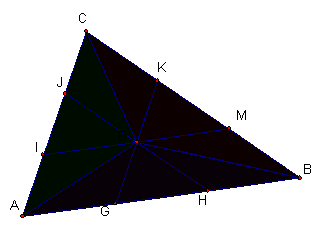
We can repeat this
construction for the other two triangles ACD and BCD. When we trisect the area
of all three triangles we see that the line HD intersects segment AC at a point
of trisection for triangle ACD. Similarly we can conclude the same for all the
lines of trisection of the triangles and we obtain the following construction.
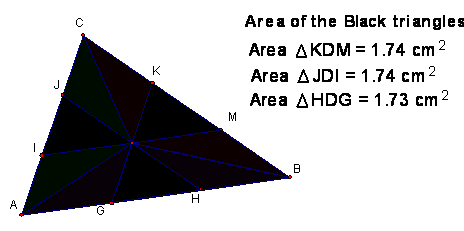
We can now apply a modified
version of the mid-segment theorem. Since CI and CM are 2/3 the length of CA
and CB, respectively, then segment IM is 2/3 the length of AB and parallel to
AB. We also know that ID = DM. Therefore ID and DM is 1/3 the length of AB and
is equal to GH. Applying the same
theorem to the other segments, GK and JH, we obtain that KD = DG = JI and DJ =
DH = KM. Now we can say by SSS that triangles DIJ, DKM and DGH are congruent
and therefore their areas are equal.
We still need to prove that
all the adjacent non-black triangles are congruent. We will start by showing
that triangles BDH and BDM are congruent. Since DM is parallel to AB and DH is
parallel to CB then DMBH is a parallelogram. Then DB is the diagonal which divides
the parallelogram into congruent triangles BDH and BDM. We can apply this same
argument to obtain the following congruencies and therefore equal area
triangles.
BDH ≈ BDM
ADG ≈ ADI
CDJ ≈ CDK
We need to make one final
claim. We know that BH and GA are both 1/3 of AB and the altitude for both
triangles is the same. Now we can claim that the area of triangle ADG and BHD
are the same. Similarly, we can claim that the areas of all the following
triangles are the same:
ADG and BHD
BDM and ADK
CDJ and ADI
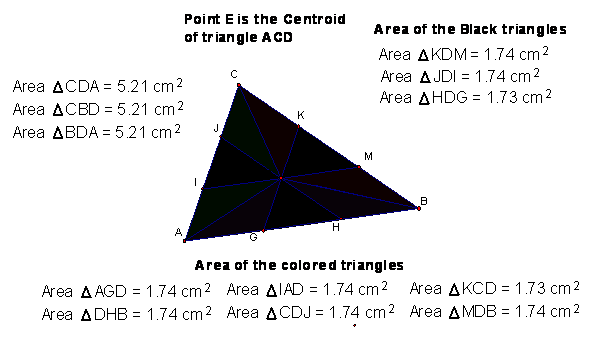
By transitivity then all the
colored triangles have the same area. Therefore triangle ABC is trisected into
three triangles all of equal area, where each triangle is made up of two
congruent colored triangles and one black triangle. Click here to see this
construction in GSP.