EMAT 6680- Final Assignment
If we construct any triangle ABC, any point inside the triangle, P, and lines from the vertices of the triangle through point P, we construct the following triangle.
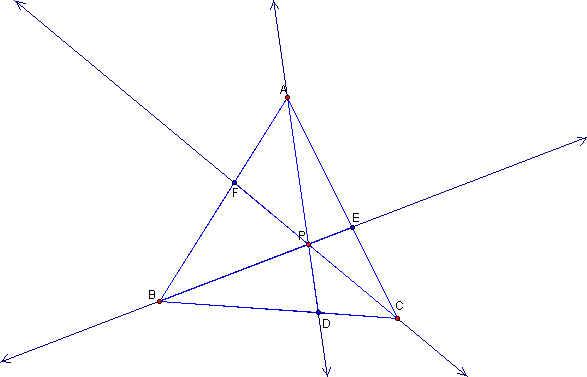
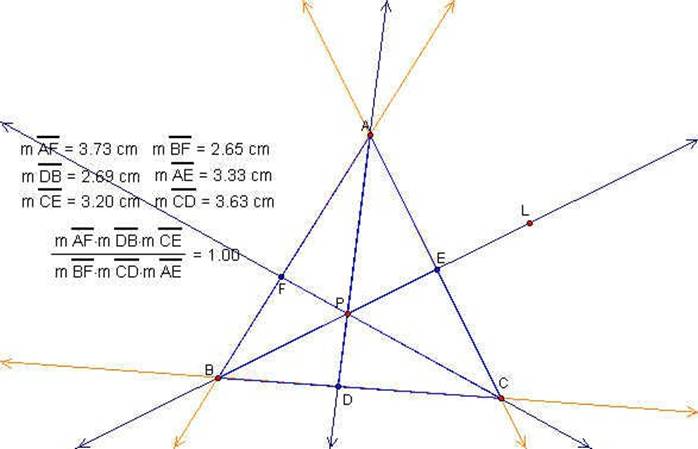
Where E, D and F are the intersections of these lines to the sides of the triangle ABC. If we consider the ratio (AF*BD*CE)/ (BF*CD*AE) we can see a relationship. The following GSP sketch shows this relationship is equal to one.
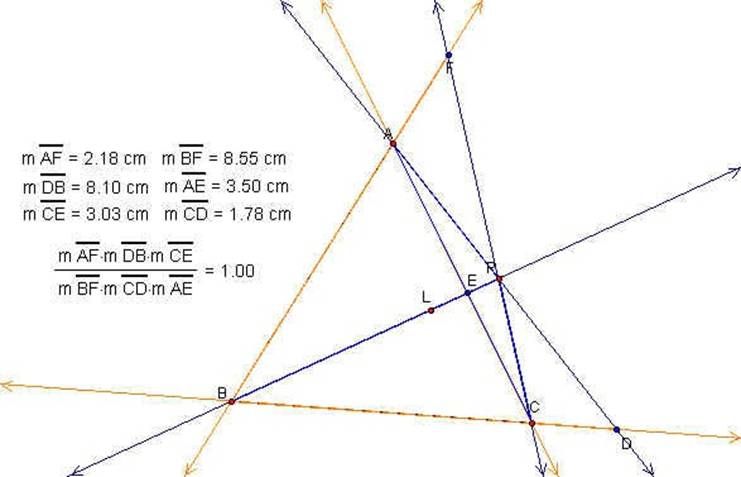
We can now check in GSP to see if this relationship holds true if P is outside of triangle ABC. We can see from the sketch below that it does in fact remain equal to one. Click here to see this sketch in GSP.
We can prove this relationship by establishing some triangle similarities. First we need to construct two lines (in green) parallel to BE through points A and C.
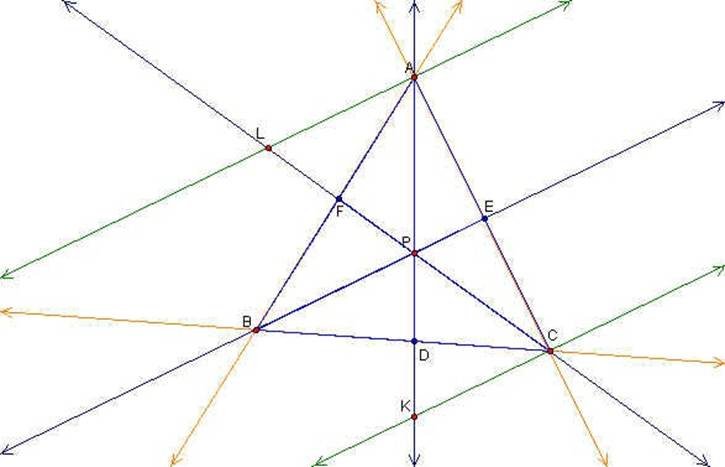
Now we can consider the triangles ACK (purple) and AEP (green). We know by the alternating interior angle theorem that these two triangles have two congruent angles and therefore are similar by angle-angle similarity. Once we establish similarity we can state the following ratio: EP/CK = EA/CA.
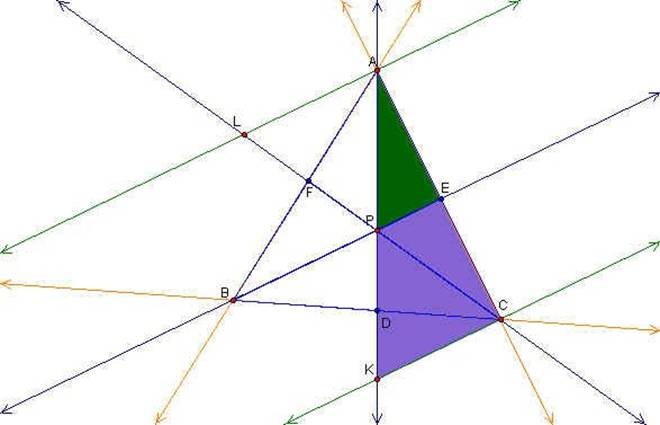
We can also consider triangles ACL (blue) and ECP (green). Again we know by the alternating interior angle theorem that these two triangles have two congruent angles and therefore are similar by angle-angle similarity. Once we establish similarity we can state the following ratios: CE/CA = EP/AL.
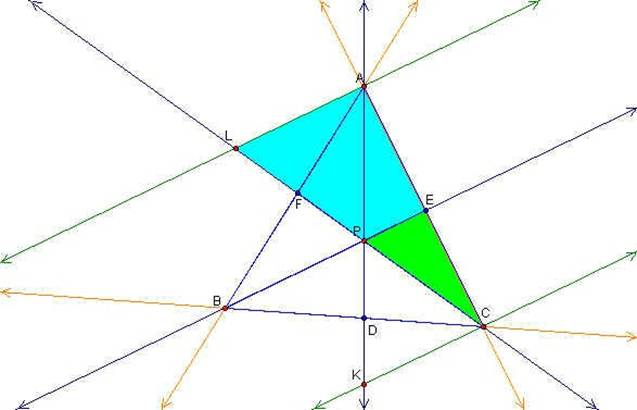
Now we need to consider two more sets of triangles, AFL & BFP and BDP & CDK, as shown below. First we can prove triangles AFL and BFP have congruent angles by the vertical angle theorem and alternating interior angle theorem. Therefore triangles AFL and BFP are similar by angle-angle similarity. We can make the same arguments for triangles BDP and CDK to prove they are similar.
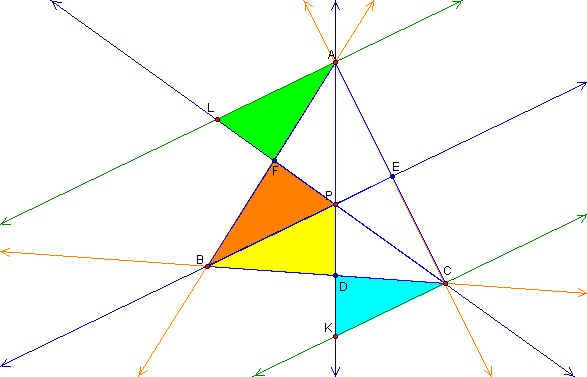
Once again we can then establish the following ratios: KC/PB = CD/BD and AL/BP = BF/AF. If we combine all the ratios established we obtain:
EP
* KC * BP *
CK
* PB *
When we simplify the equation above everything on the left side cancels out (CA on the right side cancels out too) and we obtain the original ratio
(AF*BD*CE)/(BF*CD*AE) = 1.
We can also investigate the area
of triangle formed from the original construction lines. Using GSP we can see
that the ratio of triangle DEF to triangle ABC will always be greater than or
equal to 4. Click
here to see this sketch in GSP.
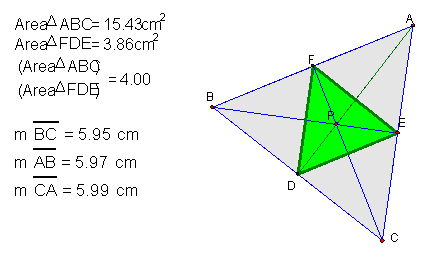
We prove this by examining triangles
ABC and DEF when the ratio is equal to 4. This occurs when triangle ABC is an
equilateral triangle. Then point P is the centroid of triangle ABC and points
D, E, F are the midpoints of the sides of triangle ABC. Since points D, E and F
are the midpoints and ABC is an equilateral triangle then segments AF, BF, CD,
BD, CE, and AE are all congruent. Also since ABC is an equilateral triangle
then angles ABC, BAC and ACB are congruent. Then by the side-angle-side
theorem, triangles CDE, AEF and BDF are congruent. Then by the side-side-side
theorem triangle DEF is also congruent to these triangles. Therefore the ratio
will be 4 since triangle ABC is divided into four congruent triangles, one of
which is triangle DEF.
We can also claim that this ratio between the areas of the triangles will be greater than 4 when point P is inside the triangle since the area of triangle DEF is maximized when P is the centroid of an equilateral triangle. When triangle ABC is an equilateral triangle and P is the centroid then the ratio of the base*height of the two triangles is also 4. As point P is moved the base*height of triangle DEF becomes smaller and therefore the ratio increases.