Assignment # 4- Centers of Triangles
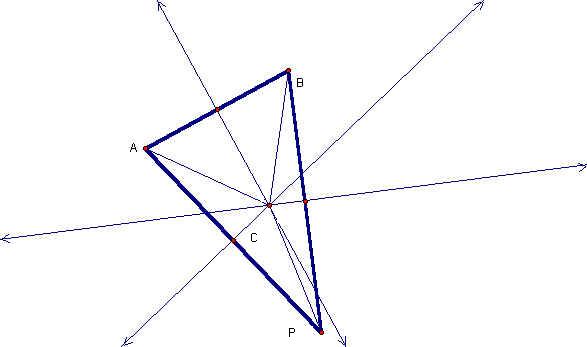
In this assignment we explored three centers of triangles. The first center we will discuss is the circumcenter. We will refer to it as point C. This center is the point that is equidistant from the three vertices of the given triangle. The circumcenter is formed by the intersection of the perpendicular lines that pass through the midpoint of the sides of the triangle. Here is a diagram of the circumcenter for triangle ABP. Click here to see this diagram in GSP.

The lengths below show that C is in fact the circumcenter and is equidistant from the three vertices.
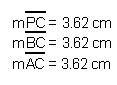
The second center we will examine is the orthocenter. We will refer to this center as point H. This point is formed from the intersection of the altitudes of the triangle. Below is a diagram of the orthocenter of triangle ABP. Click here to see this diagram in GSP.
The measurement of the angles below show that the green lines are in fact perpendicular to the sides of the triangle and are concurrent at point H.

The next point examined is the centroid. We will refer to this center as point G. This center is the intersection of the three medians. Point G is formed by the lines that pass through the vertices of the triangle and through the opposite side's midpoint. Below is a diagram of the centroid of triangle ADF. Click here to see this diagram in GSP.
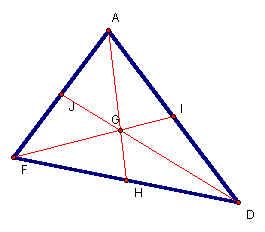
The measurements of the segments below show that points J, H and I are in fact the midpoints of their corresponding sides. This makes segments GJ, GH and GI the medians.

Now we will prove that points H, C and G are collinear and that GH = 2 GC. Let's look at the three centers on the same ABP triangle. Click here to see this diagram in GSP.
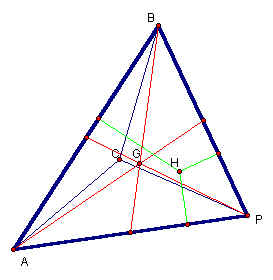
We will construct additional lines to help prove that G is on the line defined by point H and C. Once we prove that G is on the line then we need to prove that G is the centroid and is the intersection of the medians.
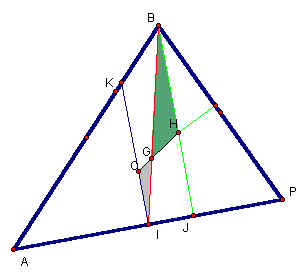
Using the construction above we can see that segments IK and JB are parallel since they were both constructed to be perpendicular to segment AP. Also we can see that segment CH and BI intersect these two parallel lines. Using the relationship of interior angles of parallel lines, we know that angles CIG and GBH are congruent and so are angles GCI and GHB. Therefore using the property of the sum of the interior angles of a triangle, we can deduce that angles CGI and HGB must also be congruent. Since angles CGI and HGB are congruent we can now state that point G is on the line produced by point CH. We can also say that triangles CGI and GHB are similar since all corresponding angles are congruent.
Now we must show that G is the centroid of this triangle.
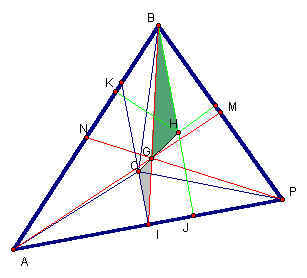
To prove this we must prove that segments GI, GM and GN pass through the midpoints of segments AP, BP and AB, respectively. First we will prove that triangles ACI and PCI are congruent. Segment CI is congruent by the identity property. Angles CIP and CIA are congruent because they are both 90 degree angles since segment CI was constructed to be perpendicular to segment AP. Since C is the circumcenter of the triangle then we know that segments CA and CP are equal. Then we know that by the Hypotenuse-Leg Theorem, triangles ACI and CIP are congruent and segments AI and IP are equal. Therefore I is the midpoint of segment AP.
We can do the same proof for triangles BCM and CMP to prove they are congruent and that point M is the midpoint of segment BP. And again with the same proof we can prove that ACN and BCN are congruent and that point N is the midpoint of AB.
Now that we know G is the centroid of the triangle we know that segment BG twice as large as GI since a property of the centroid is that G is 2/3 the distance from the vertices to the opposite sides. Having proved that triangles CGI and GHB are similar earlier we now know their ratio is 1:2. Using this ratio we can now claim that segment GH is twice as large as segment CG. Therefore 2 CG = GH.