The purpose of this assignment is to investigate the altitudes and orthocenters of triangles.
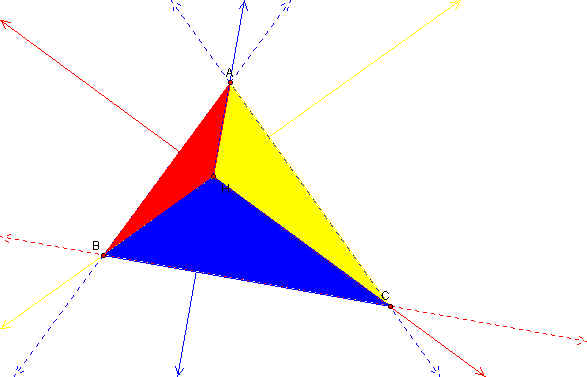
We begin by constructing any triangle ABC. We then construct the orthocenter of triangle ABC, labeled H. We construct the orthocenters for the triangles BHC, HAB, HAC. We can see from the sketch below that the orthocenters to the smaller triangles, BHC, HAB and HAC are A, C, B respectively. In the sketch below the dotted lines are shared perpendicular lines. Click here to manipulate this sketch in GSP.

If we construct the circumcircles of triangles ABC, BHC, HAB and HAC we obtain the following sketch. Click here to see this sketch in GSP.
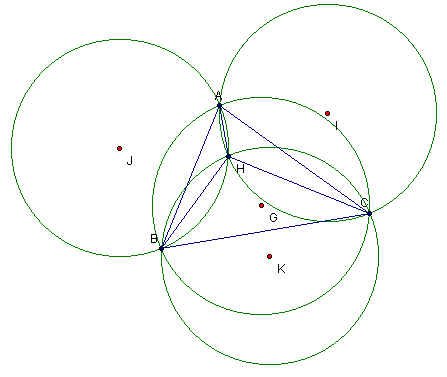
In this sketch G, K, I and J are the circumcenters of triangles ABC, HBC, HAC and HAB respectively. We can see from this sketch that the orthocenter of ABC, H, is the intersection of the three circumcircles of triangles HBC, HAC and HAB. We can also see by manipulating this sketch that as a vertex is moved to the orthocenter, the circumcircle of triangle ABC overlaps with the circumcircle of the corresponding triangles. For example if vertex C is moved to the orthocenter, H, then the corresponding triangle would be HAB. Similarly if vertex A is moved to the orthocenter then the corresponding triangle would be HBC. This overlapping occurs because triangle ABC overlaps the corresponding triangle and therefore produces the same circumcenter and circumcircle. Click here to see this animation in GSP.
We continue the investigation by constructing an acute triangle ABC. When we construct its altitudes and orthocenter, we obtain the following sketch.
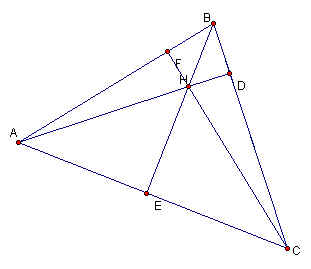
Now we will prove that HD/AD + HE/BE + HF/CF = 1 and that AH/AD + BH/BE + CH/CF = 2. We need the formula for the area of a triangle (1/2 base * height) to prove this. We begin by stating that the areas of the small triangles HAB, HBC and HAC are equal to the area of the big triangle ABC or
Area ABC = Area HBC + Area HAB + Area HAC ( Eq. 1).
We know the following:
Area HBC = 1/2 HD*BC ( Eq.2),
Area HAB = 1/2 HF*AB ( Eq.3),
Area HAC = 1/2 HE*AC ( Eq.4),
Area ABC = 1/2 BE*AC = 1/2 AD*BC = 1/2 CF*AB ( Eq. 5).
Therefore substituting equations 2, 3 and 4 into equation 1 gives
Area ABC = 1/2 (HD*BC + HF*AB + HE*AC).
Now dividing by the area of ABC gives us:
1 = 1/2 (HD*BC + HF*AB + HE*AC) / Area ABC.
Since the area of ABC can be expressed three different ways (see equation 5) we can choose the appropriate expression to use in order to simplify the equation. We obtain the following equation when we cancel out the 1/2's and substitute the appropriate area of ABC
1 = HD*BC/AD*BC + HF*AB/CF*AB + HE*AC/BE*AC.
This equation simplifies to the first equation to be proven
HD/AD + HE/BE + HF/CF = 1.
Now to prove the second equation AH/AD + BH/BE + CH/CF = 2. We can derive this equation from the first equation that was proven. We can see from the sketch that HD = AD - AH, HE = BE - BH and HF = CF - CH. Substituting these values into the equation above gives:
(AD - AH)/AD + (BE-BH)/BE + (CF-CH)/CF = 1.
Simplifying this equation gives:
1 - AH/AD + 1 - BH/BE + 1 - CH/CF = 1,
- AH/AD - BH/BE - CH/CF = -2.
And finally:
AH/AD + BH/BE + CH/CF = 2.
Click here to see the two proven equations represented in GSP.