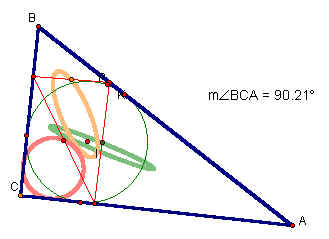
The purpose of this assignment is to investigate Pedal triangles. We begin by constructing any triangle ABC. We construct the pedal triangle by choosing any point, P, and drawing the perpendicular from point P to the sides of triangle ABC. Click here to see this sketch in GSP.

We can manipulate P to investigate the outcome if P is different triangle centers. First we move P to the incenter of the triangle. The vertices of the pedal triangle are the intersections of the perpendiculars from the incenter (in dark blue) and the sides of triangle ABC. Click here to see the animation and manipulate this sketch.
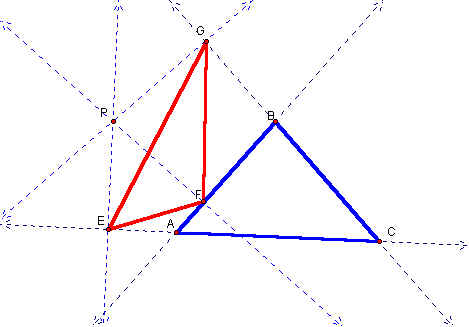
We can move P to the orthocenter of triangle ABC. The vertices of the pedal triangle are the intersections of the altitudes and the sides of triangle ABC. Click here to see this animation and manipulate this sketch.
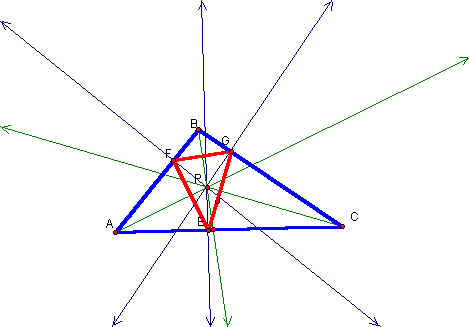
If we move point P to a side of triangle ABC, then the pedal triangle is inscribed in triangle ABC with point P being one of the vertices. Click here to see this animation in GSP.
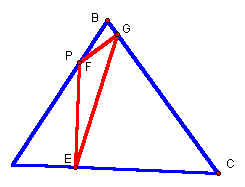
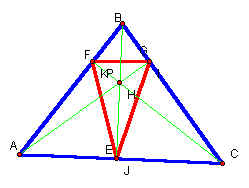
Next we can set the path of P to be the circumcircle of triangle ABC. We can see that the pedal triangle degenerates and the Simson Line (in red) is formed. If we trace the midpoints of the pedal triangle sides as point P is animated around the circumcircle we can see their paths. The midpoints follow elliptical paths which go through the midpoints (Q, R and T) of the sides. Click here to see this animation in GSP.
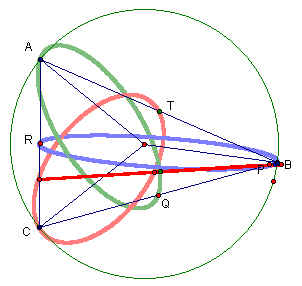
We can see from this sketch that when point P is at one of the vertices of triangle ABC the Simson Line becomes the altitude passing through that vertice. If we construct the orthocenter we can make another observation. We can see from the sketch below that the Simson Line becomes one of the sides of triangle ABC when the segment connecting point P and the orthocenter of triangle ABC intersects the sides at the midpoints.
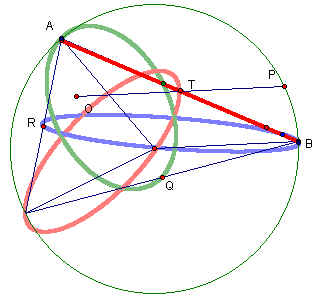
Finally if we animate point P around the incircle of triangle ABC and trace the midpoints of the pedal triangle we can see their elliptical paths. Click here to see the animation in GSP.
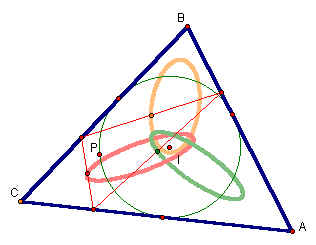
If we repeat the animation of P around the incircle when ABC is a right triangle one of the midpoints paths becomes a circle.