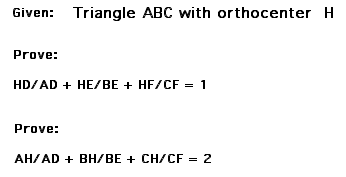
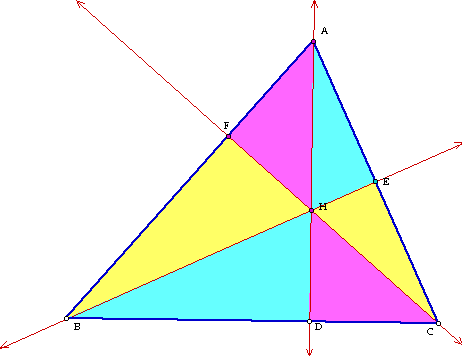
 |
 |
We want to show that given this acute triangle that when we add the ratios on the left they are equal to 1. First let's begin by finding the areas of certain triangles and comparing them to the area of the whole triangle. So let's start with ratio of the area of triangle BHC to the area of triangle ABC.
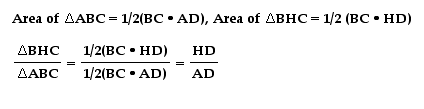
Now let's look at the ratio of the area of triangle AHB to triangle ABC.
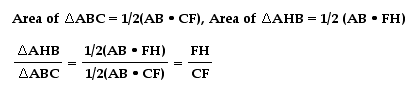
Finally let's look at the ratio of the area of triangle CHB to triangle ABC.
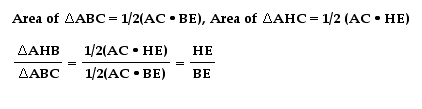
What happens if we add up both sides of the ratios of the areas??
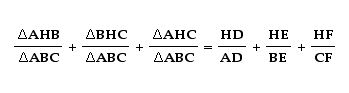
Let's simplify:
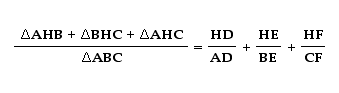
But if we look at the triangle again, we see that the sum of the areas of the three triangles in the numerator is equal to the area of triangle ABC so the left hand of the equation goes to 1 and we get the desired relation.
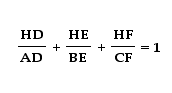
Now let's look at the second relationship.
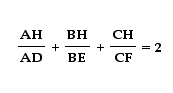 |
 |
First, let's look at the ratio of the area of triangle AHB plus the area of AHC to the area of triangle ABC.
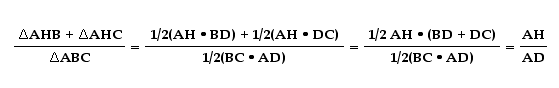
Next, let's look at the ratio of the area of triangle AHC plus the area of BHC to the area of trianlge ABC.
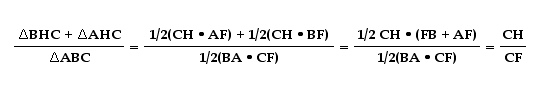
Finally, let's look at the ratio of the area of triangle AHB plus the area of BHC to the area of triangle ABC.
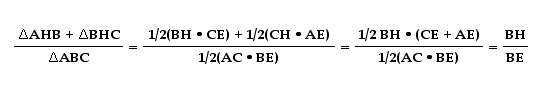
Now if we add both sides of the ratios we get,
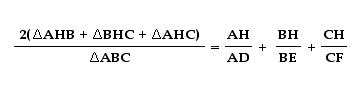
Again note that the area of triangle AHB plus the area of BHC plus the area of AHC is equal to the area of ABC. So we get the desired relation.
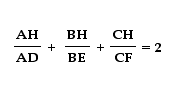
Does this relation hold for an obtuse triangle? We will use a picture to demonstrate that it doesn't.
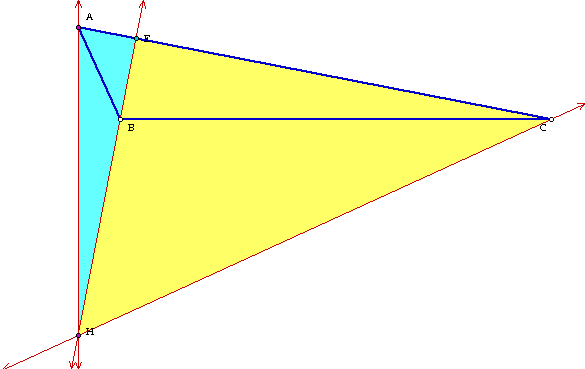
If we look closely at this picture with the orthocenter outside of triangle ABC we can see that BH is much greater than BE and HE is much greater than BE. In fact as angle ABC goes to 180 degrees BH and HE continue to grow larger. This implies that we can make BH/BE > 2 by itself and HE/BE > 1 by itself so the two statements do not hold. This concludes the proof of the statements.