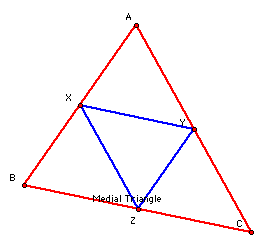
Proof:

Triangle AXY is similar to triangle ABC. This is because they share angle A, side AX is one half of side AB, and side AY is one half of AC. Therefore by SAS the two triangles are similar. The same argument can be repeated for triangle CZY and triangle CBA, triangle BZX and triangle BCA. From these three similarities we get that each of the sides of triangle ZXY are one half the length of the sides of triangle ACB and therefore these two triangles are similar. Finally since each small triangle is similar to the big triangle they are all similar to each other but they also all have the same ratio to the larger triangle and so we can conclude that they are congruent to each other.

Now to get the area relation. Since the sides of ZXY are one half the sides of ACB we know that the heights are also in the same ratio. This implies that the area of ZXY is 1/4 the area of triangle ACB Since all of the smaller triangles are congruent this implies that their areas are equal so the ratio of triangle ZXY to ABC is 1:4.

Finally we can conclude by AIA that XY is parallel to BC, XZ is parallel to AC, and ZY is parallel to BA.