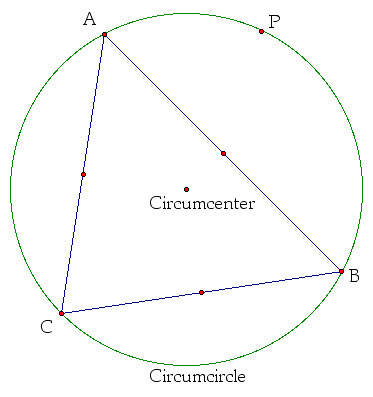
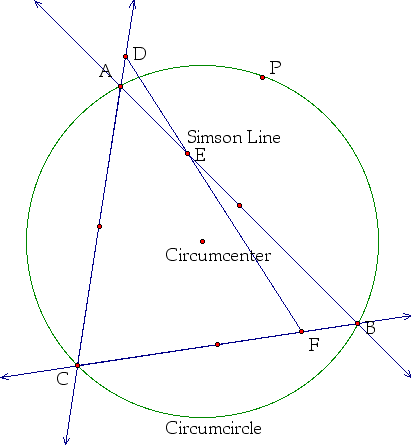
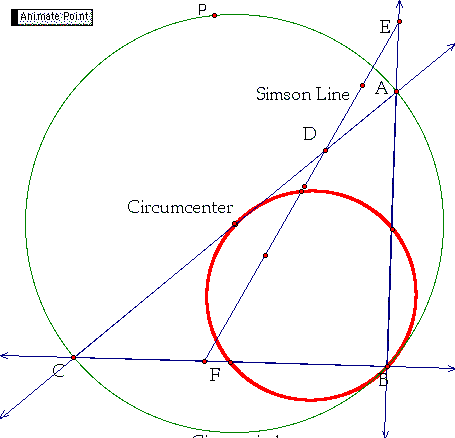
What is the Simson Line?
If we take a point on the circumcircle, call it P (as shown to the left), and then drop perpendiculars to the sides of triangle ABC (or the line extensions of sides of triangle ABC) and connect these three points, D, E, F are collinear (as shown to the right). The line formed is called the Simson Line.
 |
 |
This line is somewhat misnamed. Robert Simson (1687-1768) was indeed a geometer but no where in his writings does the proof or even mention of this line appear. Instead, it appears that an author misattributed this line to Simson some years later and the name has stuck. The actual proof appears to have been done by William Wallace around 1797. For this proof click here.
The Simson line is the degenerate case of the Pedal Triangle. The Pedal Triangle is the triangle that is formed by connecting the feet of the three perpendiculars dropped from any point in the plane to the sides of a triangle. In the case where the point is on the circumcircle of the triangle these three points are collinear.
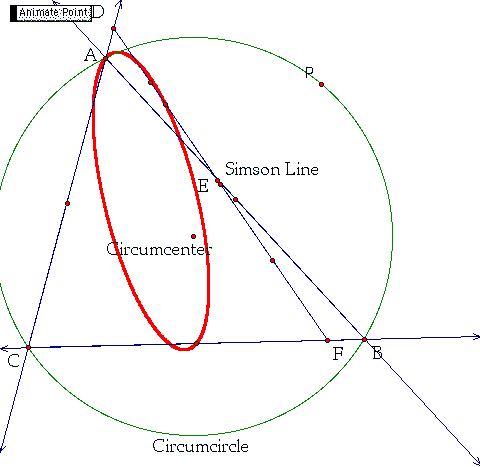
Let's look at the locus of points of the midpoints of each of the segments of the Simson Line as we move the point P around the circumcircle. First let's look at the midpoint of segment DE as P moves around the circumcircle which is shown to the left (note as P moves around the circle point D is restricted to movement along line AC and point E is restricted to movement along line AB). Second let's look at the midpoint of EF as P moves around the circumcircle (shown on the right with the first locus of points as well).
 |
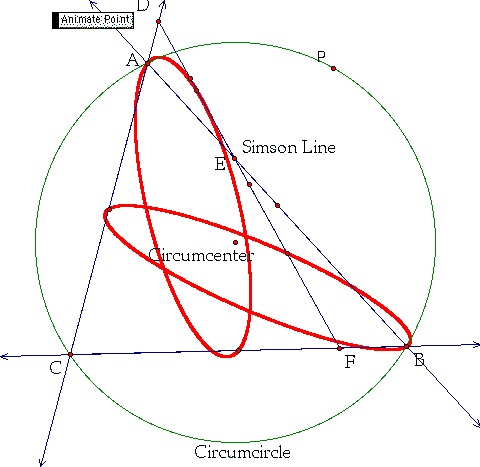 |
Both of these curves appear to be ellipses which I will leave as an unproved conjecture. What can we note about each of these ellipses? First, it appears that the width of the ellipse depends on the angle formed by the lines that the two points travel along. This observation makes perfect sense for the segment DE which travels along the rays of a larger angle gets larger itself and therefore the ellipse formed by its midpoint should be wider. The second oberservation is that each ellipse appears to go through the vertex of the angle formed by the lines that the segment is traveling along and through the midpoint of the opposite side of this angle. What happens to the Simson line at these points?
When the midpoint of DE is at vertex A of the triangle ABC, so to are the points D, E, and P. In other words, all of the points are the same point, Why? When P is at the point A then the perpendiculars to the sides AC and AB go through the point A therefore D,E are the same as A and then the midpoint of the Simson Line also corresponds to this point.
What happens to the Simson Line when the midpoint of the Simson Line travels through the midpoint of one of the segments of triangle ABC? The Simson Line becomes the same as one of the sides of the triangles. This occurs when the point P is collinear with the circumcenter of the triangle and the vertice opposite the side of the midpoint in question. Two of the points of the Simson line are the vertices of the triangle and there midpoint corresponds to the midpoint of that particular side of the triangle. (Note there is also a third ellipse created by the midpoint of DF). To download a GSP file to play with these ellipses click here.
What happens to this locus of points if the triangle has a right or an obtuse angle?
In the case of a right angle, one of the ellipses becomes a right triangle whose center is the midpoint of the segment connecting the orthocenter and circumcenter. How do we know the center? From our observations above, the circle goes through the vertice of the right angle B and through the midpoint of the side opposite angle B. In a right triangle, the orthocenter is located at the vertice of the right angle and the circumcenter or the triangle is the midpoint of the opposite side of the triangle.
Do you have any guess as to what happens when one of the angles of the triangle is obtuse?

We are back to an ellipse which has the same properties of the as mentioned above. As the angle ABC goes towards 180 degrees the ellipse at the other angles get closer and closer to being lines. In other words, there width continues to get smaller and smaller. The ellipse that we see in the picture here also degenerates towards a line as angle ABC gets close to 180 degrees but degenerates at a slower rate than the two other ellipses.