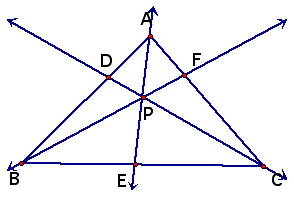
This exploration begins with the usual suspects. Given any triangle ABC and a point P inside of triangle ABC if we draw lines from each vertex of the triangle to the point P what is the relationship between AD * BE * CF and BD * CE * AF?

By having GSP measure these segments, we can verify that the relationship appears to be that AD*BE*CF = AF*BD*CE. As you can see it is true in this particular instance but to explore for yourself download this GSP file and you can change both the location of the vertices and the location of the point P and find out that it appears that the three measures multiplied together is always equal to the other three measures multiplied together.
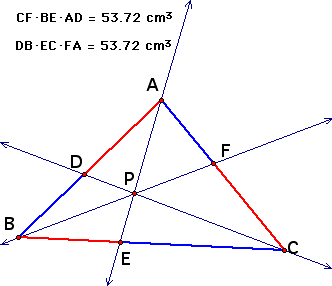
Can we come up with a proof that shows that AD*BE*CF = AF*BD*CE. Let's stick in some line parallel to line AE and see if we can't find some similar triangles.
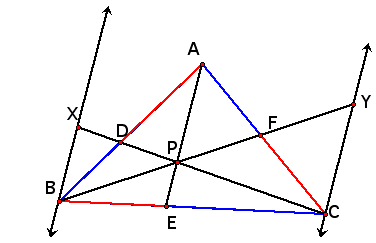
There are lots of similar triangles now to consider in this proof I will use four in particular. Note that triangle BCY is similar to triangle BEP, triangle AFP is similar to triangle CFY, triangle CXB is similar to triangle CEP, and triangle BXD is similar to triangle APD.
1) From the fact that triangle BCY is similar to triangle BEP we get that BE/BC = EP/CY.
2) From the fact that triangle CXB is similar to triangle CPE we get that CE/BC = EP/BX
3) From the fact that triangle AFP is similar to triangle CFY we get that AF/CF = AP/CY
4) From the fact that triangle BXD is similar to triangle APD we get that BD/AD = BX/AP.
Now combining these we will get some cancellation and the desired relationship.
First, note from 1) we get that EP = (BE *CY)/BC and then if we subsititute this in number 2) we get that CE/BC = (BE *CY)/(BC*BX) we can then cancel the BC's on both sides of the equations and reorganize so that CE/BE = CY/BX.
From number 3) we get that AF/CF = AP/CY or that CY = (AP *CF)/AF
From number 4) we get that BD/AD = BX/AP or that BX = (BD * AP)/AD now if we subsititute these values for CY and BX into the relation CE/BE = CY/BX (we get a nasty fraction) along with the relation we want.
CE/BE = (AP*CF *AD)/ (AP * BD * AF) the AP's cancel and we get CE/BE = (CF * AD)/ (BD *AF) or rewritten that
AF*BD*CE = AD*BE*CF
QED.
Does this relation hold when P is outside of triangle ABC?

The line segment coloring used above for your occular edification because of the orientation of the segments (for instance segment BD is a part of segment AD this time) but the relation appears to hold true. To download a GSP file to see this relation click here. By using parallel lines a similar proof works for this case. In this case, it is helpful to have parallel lines parallel to AE through points B, D, C, and F. By using some substitution and cancellation the relationship follows although it is more messy than the first so I will leave it to the reader to prove if they like.
Now let's explore the area of triangle DEF to the area of triangle ABC when P is inside of triangle ABC and see if we can come up with a relationship for this area.
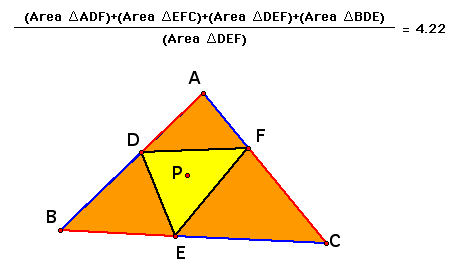
From using the sketch in GSP it appears that the area of DEF in relation to the area of ABC is always greater than or equal to 4. I have not yet figured out a proof for why it is greater than or equal to 4 but it is equal to 4 when P is the centroid of the circle and D,E, and F are the midpoints of the sides of the triangle ABC. How do we know this?
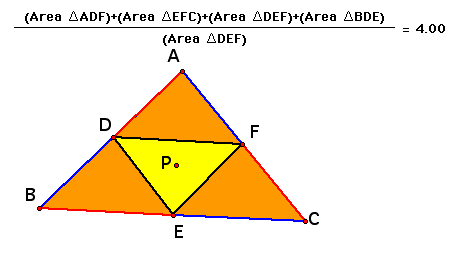
When D, E, and F are the midpoints of the sides of triangle ABC then all four of the small triangles are congruent to each other and therefore each triangle is exactly 1/4 of the area of triangle ABC which implies the ratio of the area of triangle ABC to the area of triangle DEF is exactly 4:1. In this case triangle DEF is the medial triangle of triangle ABC and point P is the centroid of both of these triangles. To explore this area relationship using a GSP file click here.