I began my investigation of quadratic equations by taking the general equation ax^2+bx+c and varying each a, b, c one at a time while holding the other two variables constant. I tried to investigate questions that I thought students might have as they used the graphing calculator software and noticed different properties as they varied a, b, c that they might not notice without the use of the software. (Please be careful to note the values on the axis as I have changed them throughout the exploration in order to demonstrate varying ideas. Because some of the ideas of this investigation include calculus arguments, I included suggestions in the mathematical discussion section for how to get students to think about some ideas for which they will not have had the formal mathematics.)
Variations of a:
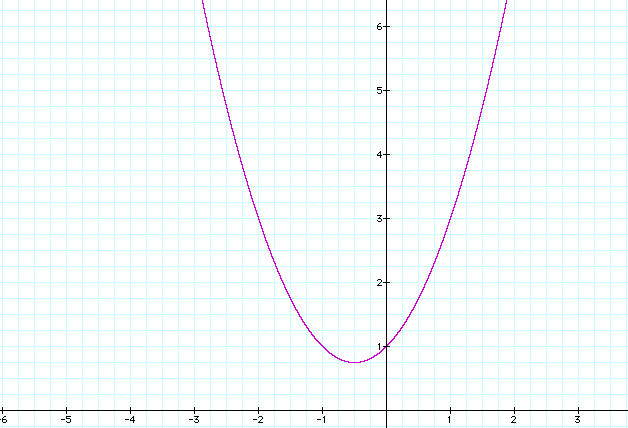
I started by setting b = 1, and c = 1 and varying a:
Let a = 1 then the graph on the left is y = x^2 +x +1. Let a = 2 then the graph on the right is 2x^2 + x + 1.
What can we notice from these graphs?
Let's try and graph a set of parabola's with a = 2, 4, 6, 8, 10 on the same axis.
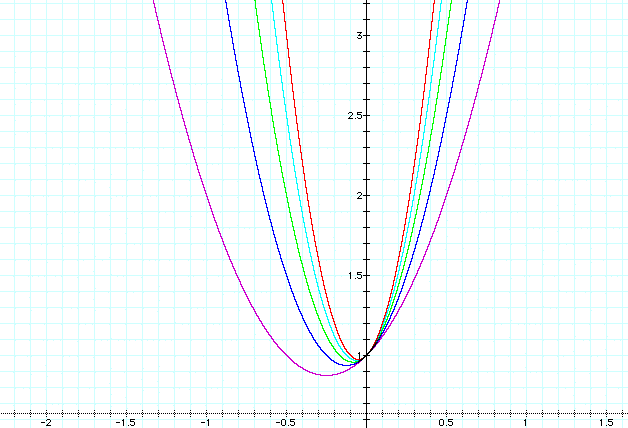
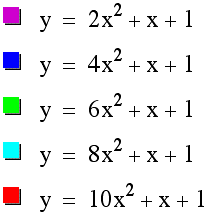
One question that comes up is will this graph ever cross the y-axis if you keep letting a be larger and larger positive values?
It looks like the graph is getting closer and closer to having a vertex at (0,1). However, if we let a get larger and larger two questions arise: will this parabola ever have a vertex at (0,1) and will it ever cross the y-axis so that the vertex has positive x values. If we restrict a to only positive values, the graph will never cross the y-axis but its vertex will tend toward the vertex (0,1). To examine why this is true click here and read mathematical discussion 1.
What happens if we let a be negative? Let's graph a = -2,-4,-6,-8,-10 and see what happens.
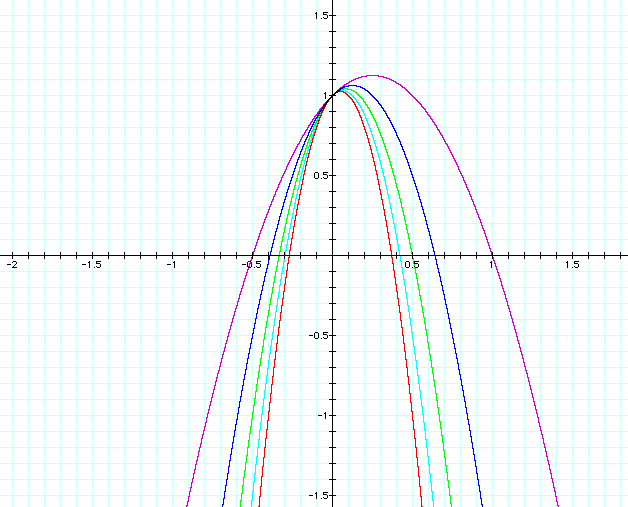
Again as a is a larger and larger negative value it looks like the vertex gets closer and closer to (0,1). However, this time the vertex is on the positive side of the x-axis. Will the vertex ever cross over onto the negative side of the x-axis? The same rationale applies here as with positive values of a except that the sign of a has changed so the graph will tend towards a vertex of (0,1) but will never cross the y-axis it. To look at mathematical discussion 1 again click here. Another thing to note about these graphs is that if we compare them to the graphs above it looks like perhaps there is some symmetry in the graphs which have equal and opposite values for a. (I will come back to this after we look at values of a that are close to zero).
We have now looked at what happens when a values get very large. Now let's think about what happens to our graph when a values get close to 0. Let's graph a = .2, .4, .6, .8, 1.0 and see what we can conclude.
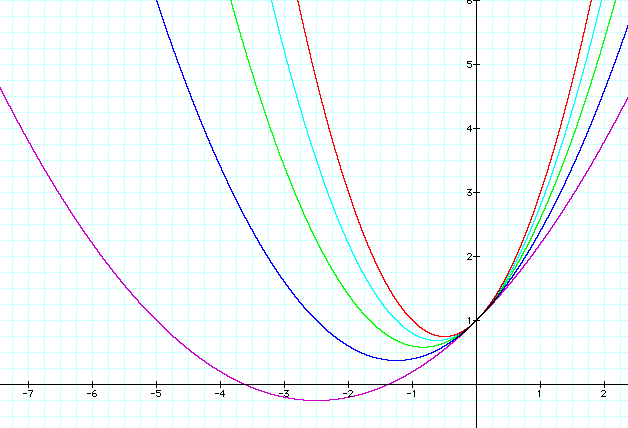
As you can see not all values of a give real roots. So when do we know when we will get real roots for the quadratic above?
The answer to this lies in the quadratic formula which gives the roots of a parabola by x = (-b+-sqrt(b^2-4ac))/2a. So in order to have real roots of the quadratic b^2-4ac >= 0 so that we get a real number when we take the square root. This means that b^2 >= 4ac In this case, when a gets small enough the parabola has two real roots (as demonstrated by the purple graph y = .2x^2 + x + 1). The parabola will have real roots when b^2 >= 4ac. We know from our specific formula y = ax^2 + x + 1 that b^2 = 1^2 and that 4ac = 4(1)a. So we get 1 => 4a or that a <= 1/4 will give our parabola two real roots. If you look at the graphs above where a is negative you will note that all of them have two real roots.
Now, let's look at the case when the a values are equal and opposite to one another. Let's try the equations with a =-1,0,1
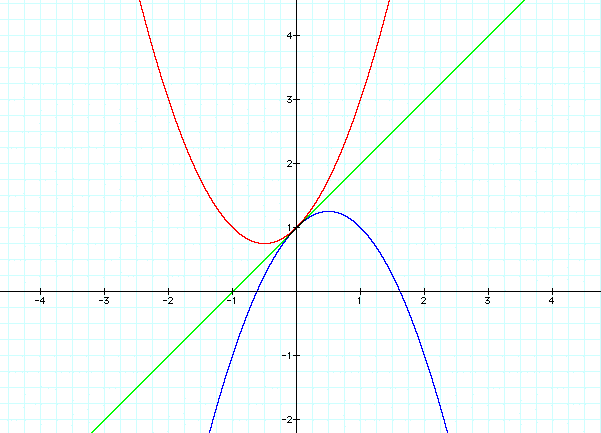
Is there some kind of symmetry in these graphs?
It appears as if there is 180 degree rotational symmetry about the point (0,1) between the parabola's that have a values that are equal and opposite. Let's look at the values of the three functions and see if we can see any patterns in the data that might lead us to that conclusion.
| X-Value | f(x)=x^2+x+1 | h(x)=-x^2+x+1 | g(x)=x+1 |
| -5 | 21 | -29 | -4 |
| -4 | 13 | -19 | -3 |
| -3 | 7 | -11 | -2 |
| -2 | 3 | -5 | -1 |
| -1 | 1 | -1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 3 | 1 | 2 |
| 2 | 7 | -1 | 3 |
| 3 | 13 | -5 | 4 |
| 4 | 21 | -11 | 5 |
| 5 | 31 | -19 | 6 |
Let's look at the data...At x = 0 all three functions are equal to 1. At x = 1, f(x) = 3, h(x) = 1, g(x) = 2. Note that the two quadratic equations are an equal distance away from the linear equation. In other words, abs(f(x)-g(x)) = abs(h(x)-g(x)) At x = -1, f(x) = 1, g(x) = -1, h(x) = 0. Again, at this point, the two quadratic equations are an equal distance away from the linear equation. This trend holds true in the general case as well. If we pick any x value the y distance from the linear equation will be the same to the two quadratics. For an algebraic proof click here and mathematical discussion 2 click here. What conditions have made this occur? In this graph we have the two quadratics with equal and opposite a values and the linear equation where a = 0. These are exactly the conditions for something to have 180 degree rotational symmetry (that all points are equidistant from a central point...in this case that point is where the three graphs intersect at (0,1)).
Variations in b:
Let's pick some equations to graph with different b values. Why don't we start with b = 10, 5, -5, -10.
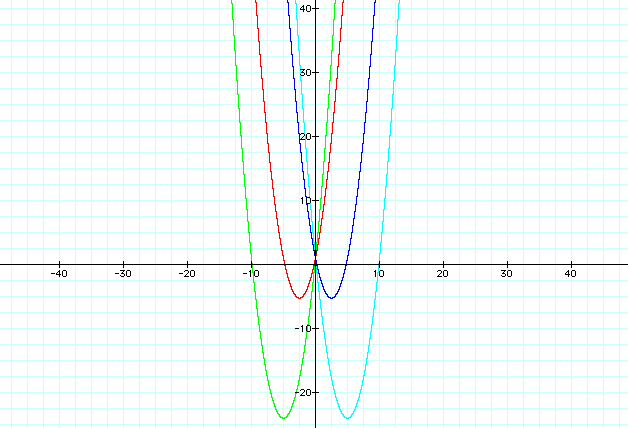
As you can see the the vertex moves up and down as b is varied. We will look at this relationship in a moment.
The other thing that we can notice is the symmetry involved when graphing b values that are equal and opposite. It appears that there is symmetry in the x-axis which would mean that (x,y) = (-x,y) for each of the points along the two equations. Let's look at the data for the graphs f(x) = x^2+5x+1 and g(x) = x^2-5x+1.
| X-Values | f(x)=x^2+5x+1 | g(x)=x^2-5x+1 |
| -3 | -5 | 25 |
| -2 | -5 | 15 |
| -1 | -3 | 7 |
| 0 | 1 | 1 |
| 1 | 7 | -3 |
| 2 | 15 | -5 |
| 3 | 25 | -5 |
If we look at the data when x = -3 then f(x) = -5 and when x = 3 then g(x) = -5. If you look at the data this is true for all points. This means that there is symmetry in the x-axis for this particular graph. Can this be extended to a general case? It can and in general if we let b have an equal and opposite value and fix a and c we will get symmetry in the x-axis. For an algebraic proof click here.
Is there any correspondence between the vertex points as we vary b? To answer this question let's look at a movie of the graphs y = x^2+bx+1 where b fluctuates between -5 and 5.
It looks like as the b value is changed that the vertex of the parabola sweeps out a parabola that is opening downward. How can we tell? One way is to watch the movie carefully and see if we can come up with the roots of the parabola (when the vertex of the parabola crosses the x-axis) and then multiply the two roots together to arrive at the quadratic equation. If you watch the movie closely, it looks as if the parabola is crossing the x-axis at the points (0,1) and (0,-1). These would correspond to the factors (-x+1) and (x+1). I choose these two factors because we know that the x^2 term must be negative because the parabola opens downward and we also want y = 0 when x = 1 and -1. If we multiply these two factors, we get y = -x^2+1 so let's add this parabola into our movie and see if it does indeed correspond to the motion of the vertex.
The point on the graph of the moving parabola is the vertex point. As you can see our guess was correct, the vertex does trace out a parabola as the b value fluctuates. As we vary the b value the vertex will always sweep out another parabola. For an algebraic proof of that click here.
Variations in c:
Let's begin again by fixing a = b = 1 and looking at the graphs where c is varied. Let's start with the graphs of y = x^2 +x + c where c = -4, -2, 0, 2, 4.
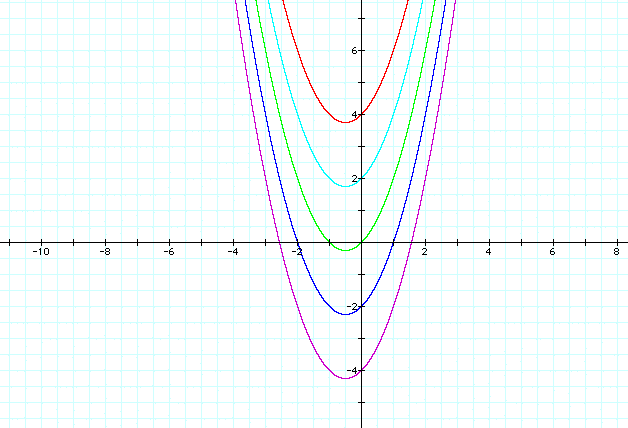
The vertex of these graphs are all at the same location. The parabolas all look to be essentially the same except for the fact that they are transposed up or down the y-axis. If we set x = 0, then we get y intercepts for each of the functions which correspond with the value we have put in for c. For example, if we let x = 0 in the function y = x^2 + x + 4 we get that y = 0^2 + 0 + 4 or y = 4. The y intercept then is (0,4). I think it is informative here (in order to see that these parabolas are transposed only up or down) to think of f(x) = x^2 +x + 4 as a composition of two functions. If we let h(x) = x^2 + x, then our function in all cases becomes f(x) = h(x) + c where we vary the values of c and this is the only change in the function f(x).