The goal of this assignment is to find two distinct linear functions f(x) and g(x) so that they are tangent to their product h(x)=f(x)g(x) in exactly two places (like the picture below).

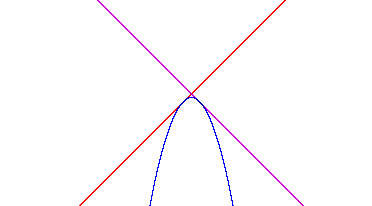
I started off using a method of trial and error by graphing two linear functions and then trying to make observations that would lead to a general case.

Trial 1:

For the first try, I selected two equations (at random) f(x)=x+2 and g(x)=x+4 making the product h(x)=(x+4)(x+2) and the graphs looks like this:

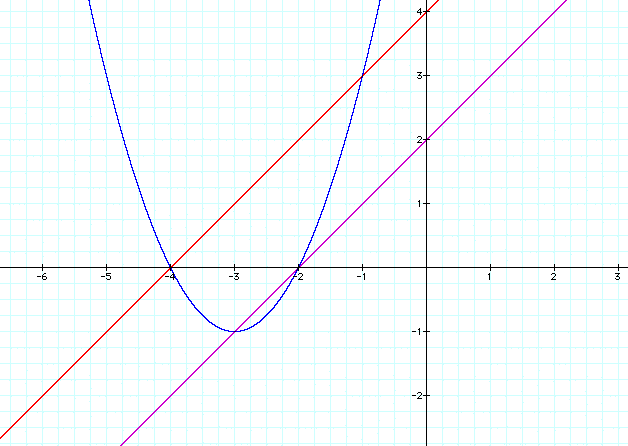
What can we note from our first try?

• From our graph it looks as if a linear function can intersect a quadratic equation at most at two points and in this case since the linear function and quadratic function are related to one another at a minimum of one place.
• The next question to ask is how are f(x), g(x), and h(x) related to one another. We know that f(x) and h(x) will intersect each other when they are both equal to zero. For if f(x)=0 then h(x)=0*g(x) and similarly this will be true for g(x) and h(x). To describe this in a graphical sense we know that the x-intercepts of the linear functions f(x) and g(x) will be sure to intersect h(x) where h(x) crosses the x axis.
• On a further note, this implies that the quadratic h(x) in question must have two real roots which means that it must cross the x-axis twice and (from the second statement) these two points must be points of interesection with the linear functions f(x) and g(x). Since we are looking for the linear and quadratic functions to be tangent in exactly two places and we know that their graphs must intersect at the x-axis we can assume that these two points of tangency must be at the x-axis.
• Finally from the first three statements, we can conclude that one of the slopes of the linear functions must be negative...so lets try again.

Trial 2:

Let's use similar values and generate a couple sets of equations. On the right f(x) = x+2, g(x) = -2x+4, and h(x) = (x+2)(-2x+4). On the left f(x) = x+2 and g(x) = -x+4 and h(x) = (x+2)(-x+4):

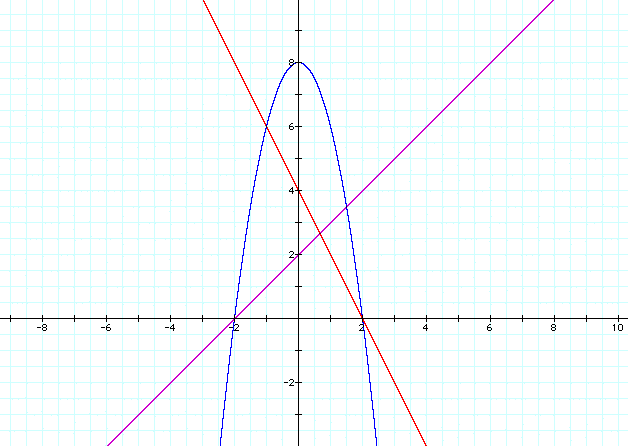
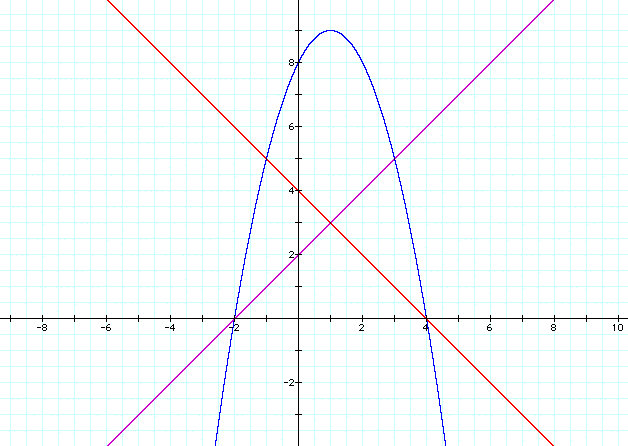
What can we note from our second try?

• The first thing to note is that the parabola has changed direction in both graphs. This is because if one of the slopes of the linear equations is negative it makes the leading term of the parabola -x^2, making the parabola open downward.
• The second thing to notice is that a parabola is symetric about the x point of its vertex co-ordinate. This means that it appears that when the slopes of the two lines are not equal (the graph on the left) there would be no way to get two points of tangency. The graph of the linear functions on the right are symmetric and therefore it appears that there is the possibility of getting two points of tangency. The graph on the left, however, does have one benefit--the parabola is symmetric about the y-axis (the line x = 0). Let's try to combine these two things (symmetry in the y-axis and equal and opposite slopes) for the next trial.

Trial 3:

We can get the parabola to be symmetric about the y-axis by making the roots of it eqaul and opposite. So let's graph the equations f(x) = x+2, g(x) = -x+2, and h(x) = (x+2)(-x+2)

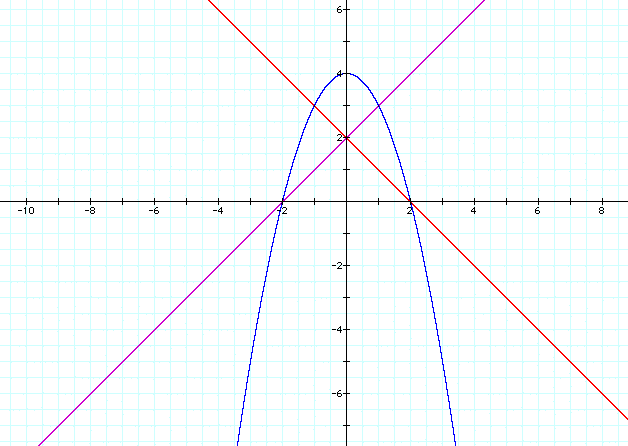
What can we note from the third try?

• It appears that the x-coordinate of the vertex is the same as the x-coordinate of the intersection point of the two lines. Let's check by setting the two linear equations equal to one another to find the intersection point:

Now let's find the x coordinate of the vertex of the parabola (the formula is x = -b/2a where h(x) = ax^2+bx+c)

So the x-coordinates of the intersection point and the vertex are equal. This in fact turns out to be true in the general case.

To see this click here for Proof 1.

• The second observation that we can make is that the vertex of the parabola must be below the point of intersection of the lines ie the y coordinate of the parabola must be less than the y coordinate of the intersection point. Students would probably just use trial and error here but it is possible to show what y values will give you a vertex below the intersection point. To see this click here for Proof 2.

Trial 4:

Now I will try to modify the above values of the y intercepts of the linear equations to see if I can get them to be tangent to the parabola (for details on the numerical values I choose look at proof 2). Let's try f(x) = x+3/4, g(x) = -x+3/4, and h(x) = (x+3/4)(-x+3/4).

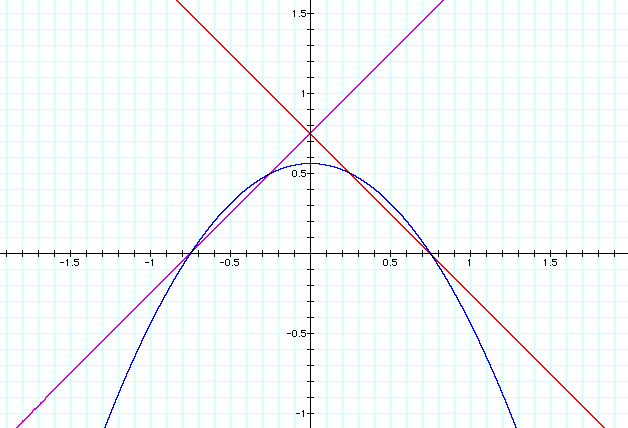
What can we note from this try?

• Were getting closer...How can we show the conditions that will give us the general case? To find out click here for proof 3. To continue pluging and chugging continue downward on the page.

Trial 5: Let's try again with the equations f(x) = x+1/2, g(x) = -x+1/2, and h(x) = (x+1/2)(-x+1/2).

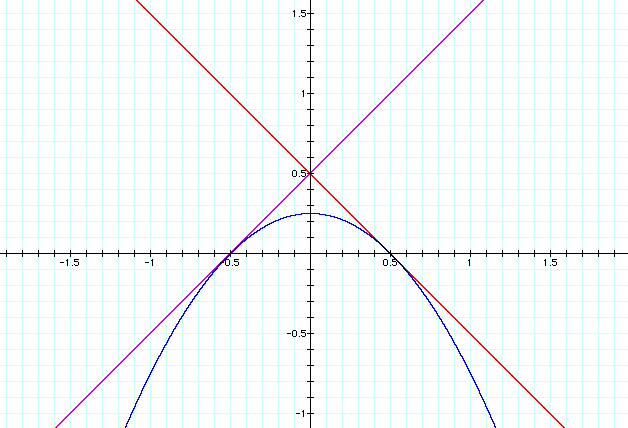
What can we note from trial 5?

• It looks like we got it!!! Let's make sure by setting the equations equal to each other.

Great they intersect at -1/2 and 1/2 (you can get 1/2 by letting g(x) = h(x)). These are the values of the x-intercepts of the linear equations and the two roots of the quadratic.

Trial 6: Let's change the slope of the linear equations and see if our functions still work. Let f(x) = 2x+1/2, g(x) = -2x+1/2, and h(x) = (2x+1/2)(-2x+1/2).

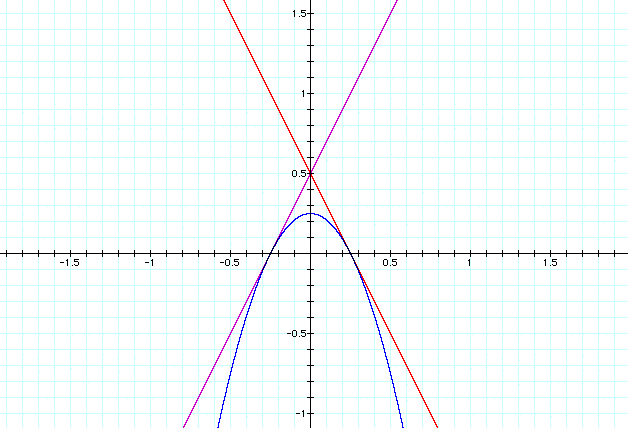
What can we note from trial 6?

• The vertex point and the point of intersection of the lines stays the same but the points of tangency between the parabola and the lines have different x values. As shown in the proofs page the slope of the equations doesn't matter as long as they are equal and opposite.

Trial 7:

Now let's check and see what happens when we change the y-intercpets of the linear equations. Let f(x) = x+3, g(x) = -x-2, and h(x) = (x+3)(-x-2) (left hand graph) and f(x) = x+3, g(x) = -x-1, and h(x) = (x+3)(-x-1) (right hand graph).

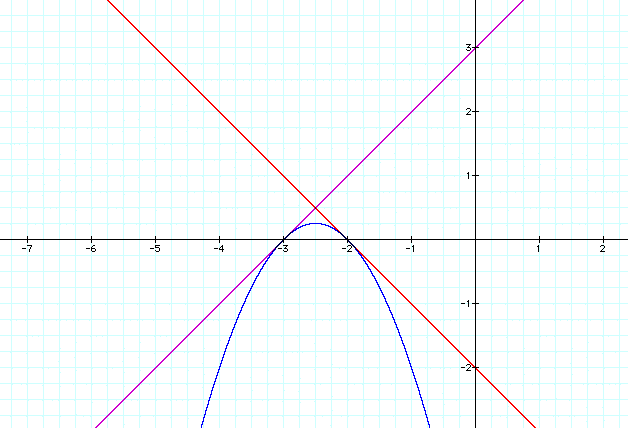
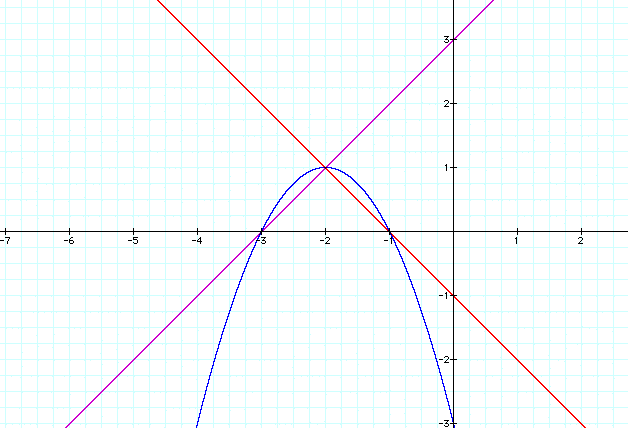
What can we note from trial 7?

• The left hand graph looks good the right hand one doesn't. Also, we have slid both graphs down the x-axis making the axis of symmetry different. Why does one graph work and the other doesn't? The answer lies in the fact that the y coordinate of the vertex of the parabola must always be 1/4 and the point of intersection of the linear equations must always be 1/2. To see this go to the proof page. From that, we get that when you add the y-intercepts of the linear equation they should equal 1. So if f(x) = ax+b and g(x) = -ax+c. This implies that b+c = 1 or that c = 1-b.
• The general equations that will give two points of tangency are f(x) = ax+b and g(x) = -ax+(1-b).