Overview:
1)Definition and history of a cycloid
2)Exploring a cycloid in GSP to get an intuitive feel about how it works
3)Looking at the parametric equations of a cycloid
1) What is a cycloid?
It is the locus of points created by a point on a circle as the circle rolls along a line.
History of the cycloid:
The cycloid was first studied by a man of the name of Cusa in his attempt to find the area of a circle using integration. Cusa lived in present day Northern Italy from 1401-1464. He was a philosopher interested in the study of the infinite, seeing the circle as the limit of regular polygons. He attempted to find the area of a cycloid using his idea about the area of circles although did so unsuccessfully. The first person to properly define a cycloid was a Frenchman by the name of Marsene (1588-1648). His other mathematical interests included numbers of the form n = 2^p - 1 where p is a prime number. In 1599, Galileo named the cycloid and after studying its form for forty years, unsuccessfully calculating the area he wrote to several other mathematicians and so began a lengthy dialogue about the properties of a cycloid.
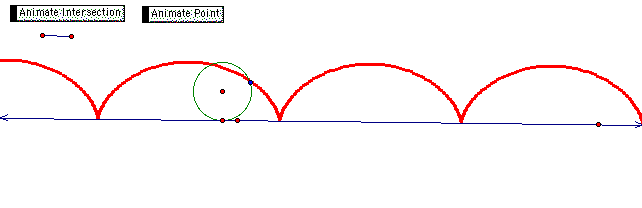
2) Let's look at a GSP construction of a cycloid.

The blue point in the diagram is the point on the circle which is being traced as it moves along the circle. One point to be careful about when doing the GSP construction is that as your point rotates around the circle make sure that it is rotating in the same direction as the direction your circle is traveling along the line otherwise you will get "an upside" down cycloid or a brachistochrone. For a GSP file to investigate this yourself click here.
What can we note from the GSP construction in terms of translating this into parametric co-ordinates?
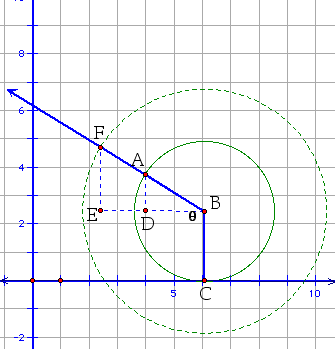
First, if we assume the radius of the circle is r, then we know that the height of the cycloid or y-co-ordinate in the parametric equation needs to fluctuate between y = 0 and y = 2r. We also know that the graph is periodic and that its period is 2 * pi * r. We need to also incorporate the motion of the circle along the straight line in our equation. What equation can we use to get this period and also take into account the movement of the circle? Let's look at the picture in GSP superimposed on a Cartesian Co-ordinate system.
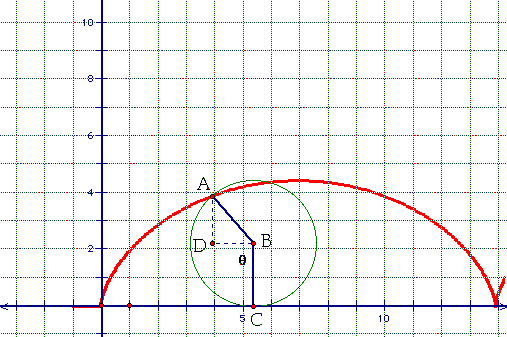
First, note that A is the point making the cycloid, radius BC is perpendicular to the x-axis, angle ADB is a right angle, and that theta is equal to angle ABC and can vary between 0 and 2 pi. So we get that the x co-ordinate should be equal to arc length AC minus the length of segment DB.
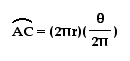 and
and
![]() so we get
so we get ![]() but how can we be sure that we are always subtracting DB because
when A is greater than half way we should be adding. This works
out though because sine is positive between 0 and pi and negative
between pi and 2 pi.
but how can we be sure that we are always subtracting DB because
when A is greater than half way we should be adding. This works
out though because sine is positive between 0 and pi and negative
between pi and 2 pi.
Now, let's think about the y co-ordinate of the graph. The y co-ordinate should be equal to segment BC plus segment AD
![]() and
and
![]() but now we have the trouble of
the sign of cosine. Since we want to be adding segment AD when
A lies in the range between pi/2 and 3pi/2 and subtracting AD
when A is between 0 and pi/2 and 3pi/2 and 2 pi we must take into
when the cosine function is negative and when it is positive.
Cosine is negative from pi/2 to 3pi/2 and is positive between
0 and pi/2 and 3pi/2 and 2 pi so we get
but now we have the trouble of
the sign of cosine. Since we want to be adding segment AD when
A lies in the range between pi/2 and 3pi/2 and subtracting AD
when A is between 0 and pi/2 and 3pi/2 and 2 pi we must take into
when the cosine function is negative and when it is positive.
Cosine is negative from pi/2 to 3pi/2 and is positive between
0 and pi/2 and 3pi/2 and 2 pi so we get ![]() .
.
3) Investigating the parmetric equations.
This gives us are parametric equations. Let's use graphing calculator and make sure that these work out alright (I have substituted t for theta because of the way graphing calculator is set up).
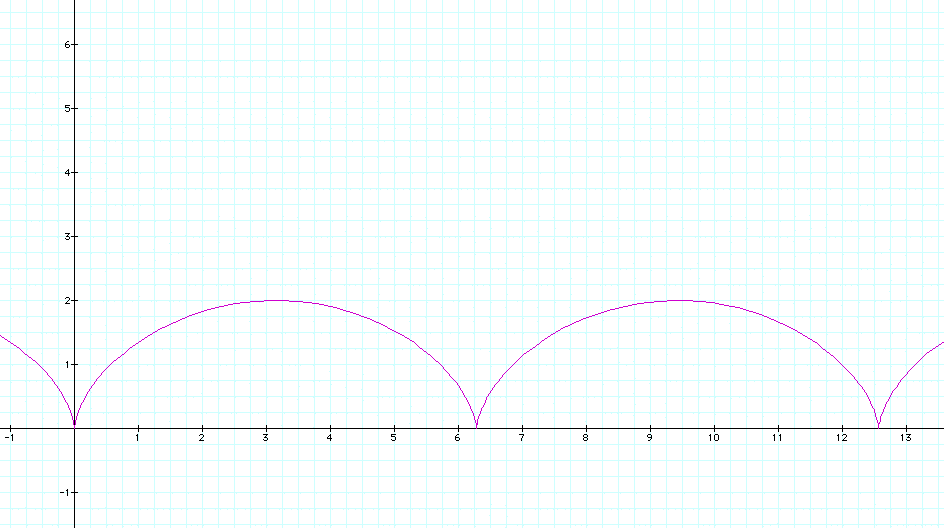
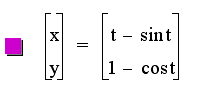
It looks like we got it!!! This is an example with the radius equal to 1. If the radius of the original circle is bigger than one then we simply mulitply both equations by the value of the radius and we get a period that is greater as well as a maximum height that is higher. In fact the period should be equal to 2 * pi * r and the height equal to 2 * r.
Now let's look at what happens when we manipulate these parametric equations in various different ways. For instance what happens when we multiply the first term of each equation by the same number and the second term of each equation by a different number. In other words, let's look at equations of the form below:
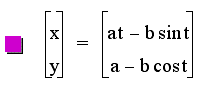 Where
we allow a, and b to be different values.
Where
we allow a, and b to be different values.
First let's let b > a and see what happens. How about if b= 1.5 and a = 1 what graph do we get?
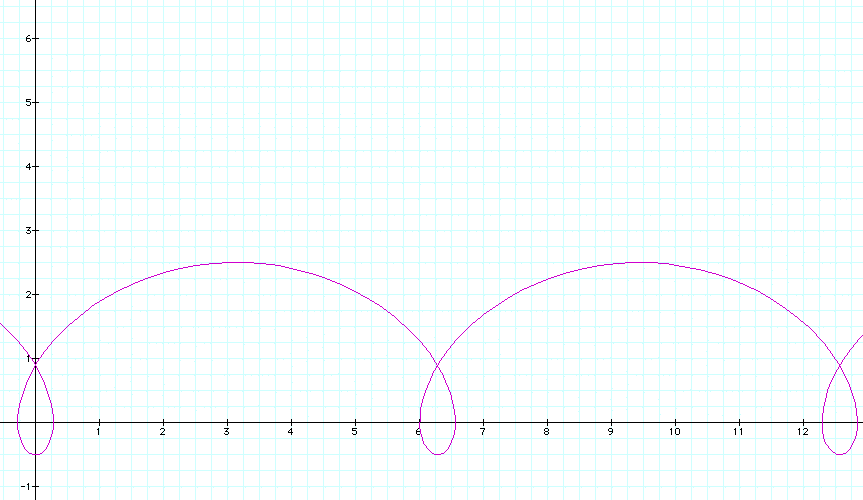
We get a part of the graph that looks like this. How can we explain this in terms of the definition of a cycloid. If b > a, then we have the locus of points created by a circle traveling along a line and a point that lies on a circle with a larger radius than the circle traveling along the line. The reason for the ray in the picture is if you use GSP to set up this construction you have to make sure that the point on the outer circle is moving at the right speed in relation to the rate of speed of the smaller circle along the line. A graph with similar characteristics would be made by tracing point F on the outer circle.
 As you can see deriving this equation would be similar
to the dervation of the first equation but would also include
the radii of the larger circle. I will leave this derivation up
to the reader. This type of cycloid is called a hypocycloid.
As you can see deriving this equation would be similar
to the dervation of the first equation but would also include
the radii of the larger circle. I will leave this derivation up
to the reader. This type of cycloid is called a hypocycloid.
What happens if a > b? Let's look at a =1.5 and b = 1.
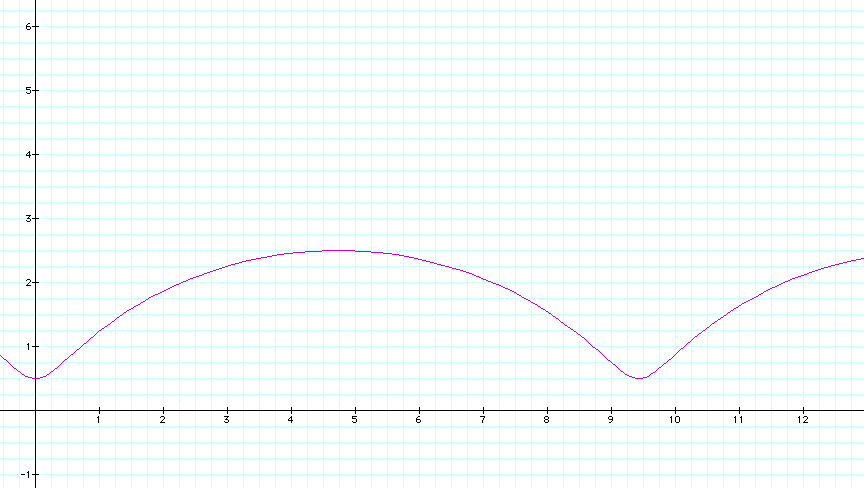
We get a slightly different path here. Instead of having a path that goes below the x-axis, the path stays above. This graph corresponds to the locus of points of a point on a circle with smaller radius than the circle that is in motion along the line. As shown below:
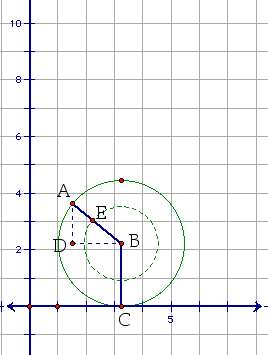 Where the graph
is made by tracing the point E as the larger circle moves along
a line. Again, allowing E to always lie on segment AB allows for
E to be moving at the same speed as the larger circle. This type
of cycloid is called an epicycloid. For final comparison let's
look at all three of these graphs on the same axis.
Where the graph
is made by tracing the point E as the larger circle moves along
a line. Again, allowing E to always lie on segment AB allows for
E to be moving at the same speed as the larger circle. This type
of cycloid is called an epicycloid. For final comparison let's
look at all three of these graphs on the same axis.
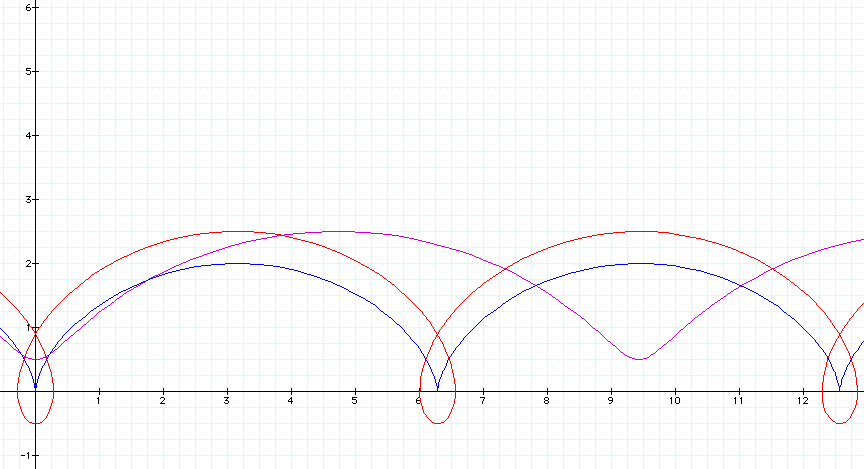
Interestingly enough the period of the hypocycloid and the cycloid are the same but the period of the epicycloid is greater. Also, note that the greatest y-value achieved is the same for the hypocycloid and the epicycloid and is greater than the greatest y-value of the cycloid. For now this finish the discussion of cycloids.