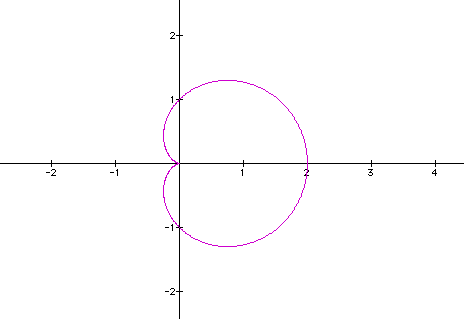
This is an exploration of the equation r = a + b cos (kø) (if you use graphing calculator or any other software you should use theta instead of phi).
First let's set a = 1 and b = 1 and vary k and see what happens. First let's look at k = 1.
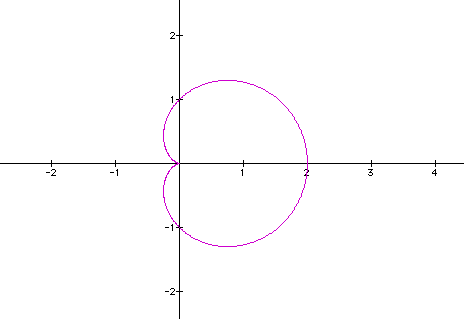
We get a cartoid. What happens if we let k = 2 (on the left) or k = 3 (on the right).
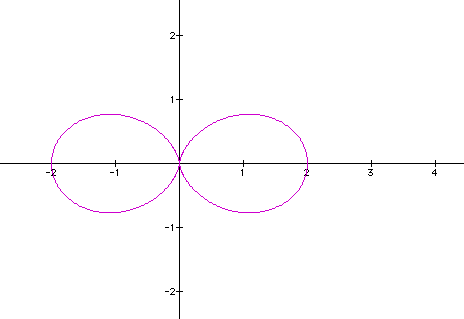
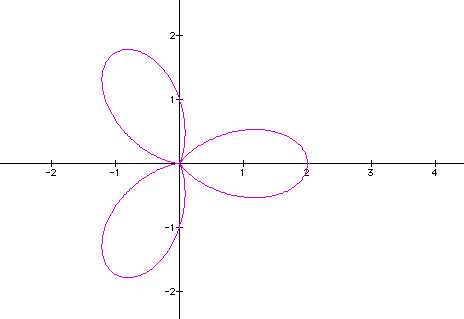
It appears that each time we put in an integral value for k we get a "flower" figure with the number of petals equal to the k value. Also note that the maximum distance of the function from the origin occurs at exactly r = 2 which makes sense since the maximum of r = 1 + 1(cos kø) = 2. This means that the curve is tangent to the circle r = 2 in exactly k places. For animation see below.
This is the animation for k = 0 to 10. When k = 0 then the graph is simply the circle r = 2 and then for the integral values of k we get a flower with exactly k petals.
Now let's try varying a and see what happens. Let's let b =1 and k = 5 and for this first graph have a = 2.
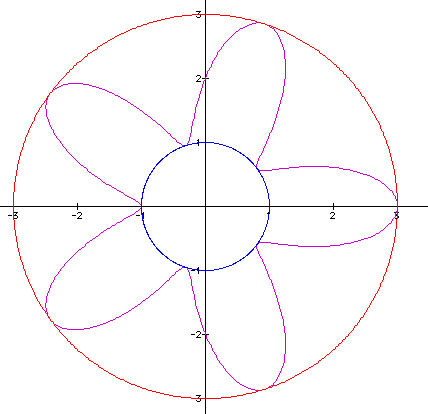
When we let a = 2 notice that the petals no longer meet at the origin. Instead the graph is moved further outward and the maximum this time is 3 so the graph is tangent to the circle r = 3 in five places. We also know that the minimum of the graph of r = 2 + 1 cos 5ø is at 1 so this time we get a circle which interior to the curve that is tangent to the graph at five places and the circle has the graph r = 1. This trend hold for all a > 1 but what happens if a < 1.
Let's set k = 5, b = 1, and a = .5 and see.
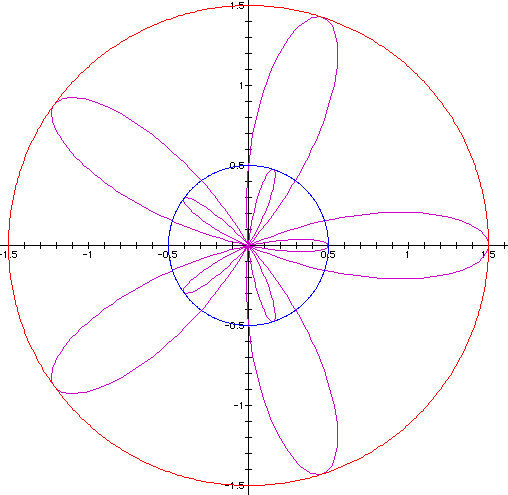
This time the we get a total of ten petals on the flower five of which occur at the minimum of the function and the other five which occur at the maximum of the function. Again they are all tangent to the circles at these points. In fact this trend of having twice as many petals as the k value occurs any time a < b. Shall we try another graph and see that this is the case. This time let's keep k = 5 and let b = 2 and a = 1.
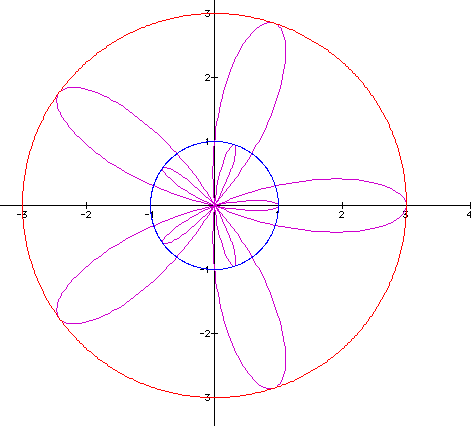
This time we get the maximum of the function being at the circle r = 3 and the minimum at r = 1. Again we can get this from the values of r = 1 + 2cos(5ø) where we can see that the maximum is three we get that the minimum to be at -1 but this still corresponds to the circle r = 1. We now have a sense of what happens if we vary a,b,k in the equation r = a +b cos (kø).