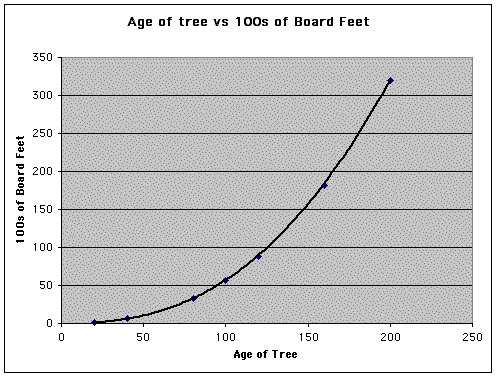
This exploration begins by looking at the data of the age of a tree and the estimated amount of board feet the tree will produce. The data is as shown below.

Age of Tree	100s of Board Feet
20	1
40	6
60
80	33
100	56
120	88
140
160	182
180
200	320

This data appears to be a power relation so let's begin by looking at the first data point and fit it to the equation y = cx^b. We get that 1 = c(20)^b. Let's try playing with the constants b and c to see if we can them to fit the data. First, we note that 20 is much greater than 1 so either b < 1 or c < 1. Let's begin by putting b = 1/8 and c = 1.

Age of Tree	100s of Board Feet	y = 1x^1/8
20	1	1.45421543344895
40	6	1.58583317513724
60		1.66827985773183
80	33	1.72936334020426
100	56	1.77827941003892
120	88	1.81927208510626
140		1.85466725539931
160	182	1.88588409508057
180		1.91385514119661
200	320	1.93922744748686

Looking at this trial we see that the first point of data is approximately 1.45 which is pretty close for the first data point but the other data points are far off. This make sense though because if our first data point is 20 taking the eighth root of that should be close to 1. However, the same applies for taking the eighth root for 200 which is equal to the eighth root of 20 and multiplying it by the eighth root of 10. So it appears that the exponent is too small. What if we leave c the same but put b = 1/2.

Age of Tree	100s of Board Feet	y = 1x^1/2
20	1	4.47213595499958
40	6	6.32455532033676
60		7.74596669241483
80	33	8.94427190999916
100	56	10
120	88	10.9544511501033
140		11.8321595661992
160	182	12.6491106406735
180		13.4164078649987
200	320	14.142135623731

The first data point is now too high with the second one close to being what it is supposed to be and the other data points are all too high. It looks like we are going to have to do some fiddling with c because if we only allow b to get bigger and hold c constant the first data point looks like it will get further away from the correct value while the other data points may get closer to the correct values. So let's try with a c = 1/8 and b = 1 this time and see what happens.

Age of Tree	100s of Board Feet	y = 1/8x^1
20	1	2.5
40	6	5
60		7.5
80	33	10
100	56	12.5
120	88	15
140		17.5
160	182	20
180		22.5
200	320	25

This time our data is pretty close for the first and second point and progressively further away as we get larger. So in order for the data to get closer to what it should be either b or c needs to be greater since allowing b to be small didn't work let's let b get slightly larger and put c to be much smaller and see if the data gets any closer. Let's let b = 2 and c = 1/128.

Age of Tree	100s of Board Feet	y = 1/8x^1
20	1	3.125
40	6	12.5
60		28.125
80	33	50
100	56	78.125
120	88	112.5
140		153.125
160	182	200
180		253.125
200	320	312.5

It looks like maybe this is the ticket. The first two data points are off by more than they were in the last trial but not by much and the later data looks like it is a lot closer to what it should be. Let's make b a little bit bigger and c smaller and see what happens. Let's put b = 2.5 and make c = 1/1750.

Age of Tree	100s of Board Feet	y = 1/1750x^2.5
20	1	1.0222025039999
40	6	5.78245057859361
60		15.9345600529677
80	33	32.7104801279969
100	56	57.1428571428573
120	88	90.1394837494215
140		132.520187141431
160	182	185.038418514995
180		248.395208471977
200	320	323.248814256707

Hey!!! Looks good. The data is just about right. It is not perfect but it is pretty close which is generally all we can hope for when we are looking for real world data.

Let's use some algebra to see if we can solve for the exact equation and see how close our equation is to the one that we solve for. There is a bit of a trick involved in solving this equation algebraically. The two equations to start with are for the first two data points so 1 = c * 20^b and 6 = c * 40^b. First, note that from the first equation we can solve so that 20^b= 1/c. We can now substitute this into the equation for the second data point but first we need to re-write the second equation like so 6 = c * 20^b * 2^b. Then with the substitution we get 6 = c *(1/c) * 2^b so with cancelation we get 6 = 2^b. Now to solve for b we need to use logarithms and we get log (6) = b log (2) and that b = log (6)/ log (2). Calculating this value we get b = 2.58 (approximately). Now we can put this back into the first equation and we get that c * 20^2.58 = 1 so c = 1/20^2.58 or c = .00044 (approximately). Above the c we used was c = .00057. We were close using our trial and error method and in fact if we used the second and third points in the data to get our values using algebra we would get an equation that had b and c almost exactly to what we calulated using trial and error. The algebra in this case gives different answers depending on the data points that we use (this often happens with real world data). Now let's see if we can get excel to fit the data to a curve.

Indeed if we graph the data using Excel, it gives a good fit for the curve if we use a power relation. The down side of fitting the curve right away is that students don't get a feel of how the equation works only that the computer can fit the data for them. In addition, the computer does not give the equation it used to fit the curve.