It has become standard practice to examine the roots of different quadratic equations. The standard way of doing this is teaching students to factor equations or if the equations are unfactorable (or a student can't figure out how to factor them) to have the student use the quadratic formula to find out what the roots are. Then graphs of different parabolas are used to show that a root corresponds to the place where the graph crosses the x-axis (when y = 0). With new graphing technology there are several new ways to look at the roots of parabolas in more general cases.
First, let's look at the more standard way of looking at different roots of a parabola by examing some quadratic equations where we look and see where the parabola crosses the y-axis. Let's take y = ax^2 +bx +c where we vary the b values of the equation (I choose to start with b since every parabola can be written with rational coefficients where we divide through by a in other words y = x^2 +(b/a)x + c/a).
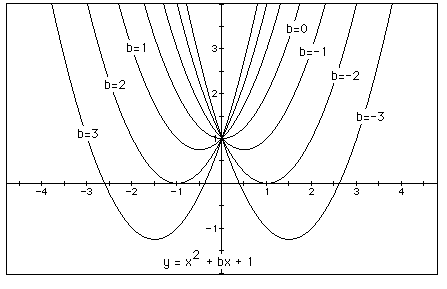
Let's graph the equation y = x^2 +bx + 1 with b= -3, -2, -1, 0, 1, 2, 3.

As you can see we can now look and discuss the roots of each equation (when doing this demonstration in front of students I would graph each of these equations one at a time until the students got a sense of where each graph should go). For an in depth treatment of this standard way of looking at roots and what happens to the equation y = ax^2 +bx +c as we vary a, b, c Click Here.
Now let's try a slightly different way of looking at these roots. Let's look at the whole class of roots in the xb plane. What I mean by this is let's graph the equation 0 = x^2 + bx + c where we change our dependent variable to b instead of having it be y. Let's use a similar equation as above, 0 = x^2 + bx +1.
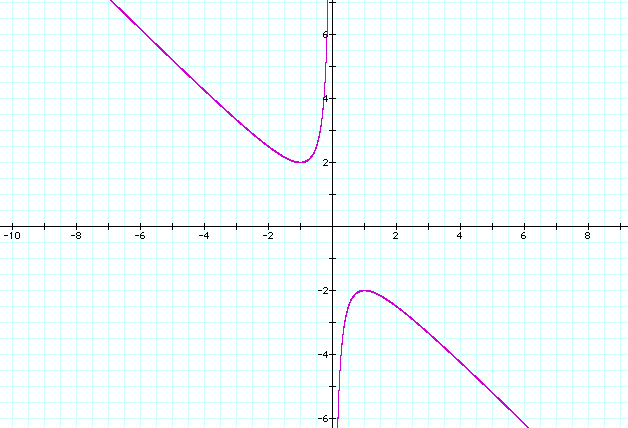
How does this graph correspond to the first graph? Let's take the graphs where b = 1, 2, 3 and put them on this graph and compare the first graph to this one.
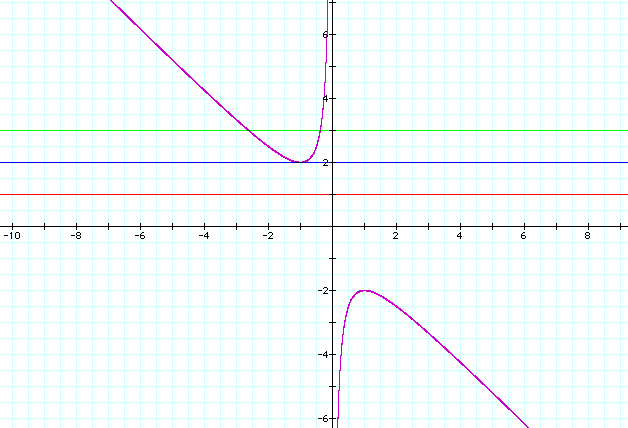
If you look at these graphs compared with the first, we see that the line b = 2 corresponds to the graph y = x^2 + 2x +1 with a double root at x = -1. In this graph, the intersection points of the line and the hyperbola are the x-values of the roots of a particular equation. The graph at b = 3 corresponds to the graph y = x^2 +3x +1 where on the standard graph we can look that the parabola has two roots and on this graph we can see the parabola has two roots because the line b = 3 intersects are hyperbolic graph in two points. In other words, this second type of graph allows us to look at the pattern of the roots rather than directly looking graph by graph at what happens when we vary the b value. We can see in this particular equation that when b < -2 or b > 2 it gives us two roots, when b = 2 or -2 we get one real root (a double root), and when -2 < b < 2 we get no real roots. This type of graphing also allows us to look at graphs as we vary b and c at the same time. Let's try that.
If we overlay the graph the equation 0 = x^2 +bx -1 onto our original graph we get
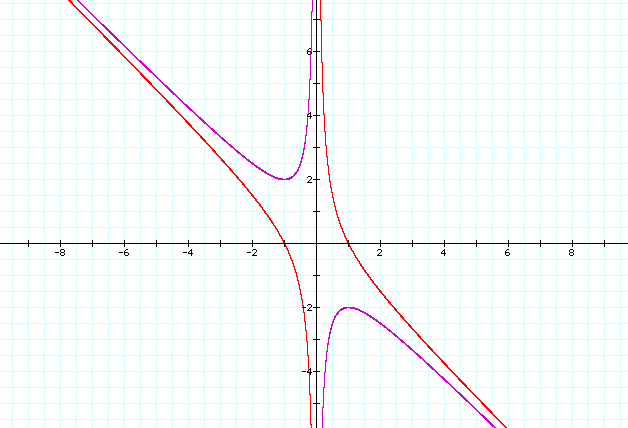
Here we see that the graph 0 = x^2 +bx-1 always has two real roots. Why is this? If we look at the quadratic formula, which is -b+-SQRT(b^2-4ac)/2a. The portion in the square root will always be greater than zero if c is negative and a is positive so we always get real roots. Also, if c is negative in the equation y = ax^2 +bx - c it will never factor to the form (x+c)^2 or (x-c)^2 because in either case c then becomes a positive value.
Now let's look at the graphs with a number of c values. 0 = x^2 + bx + c where c = -2, -1, 0, 1, 2
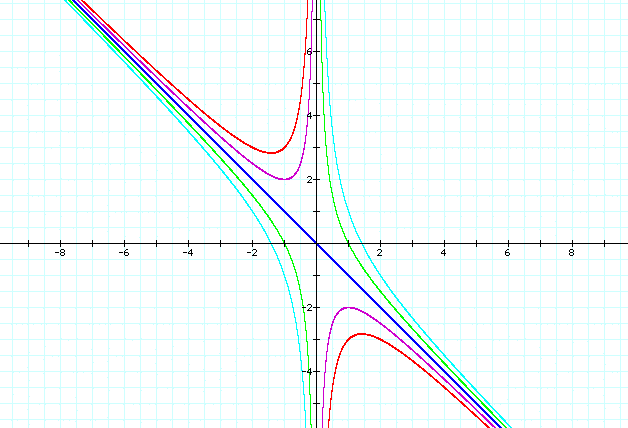
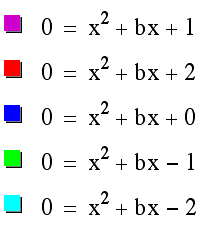
As you can see when c = 0 we get a line at y = -x and this appears to be the one of the assymptotes of the hyberobola's. The other being the y-axis. Also we can observe that if the c value is negative in the equation we always get one positive and one negative root. On the other hand if the c value is positive and you have a value of b where you get two roots they always have the same sign.
Now let's look at these graphs in the xc plane and see what happens.
Let's begin with the equation 0 = x^2 + x + c and see what we get.
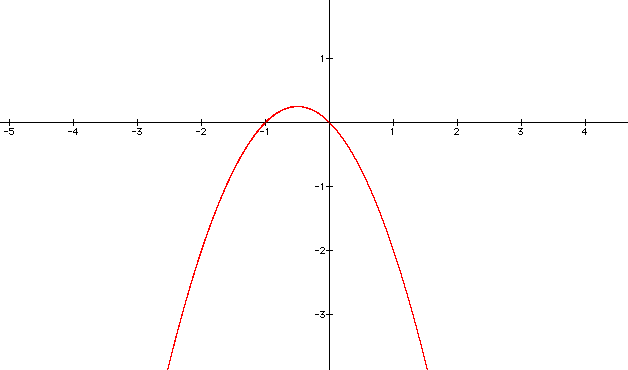
Again, if we draw a horizontal line we get the values of the roots at that particular c value. In this equation if we put c = -1/4, we get one real root (a double root). If we put the value of c < 1/4 we get two roots and if c > 1/4 we get no real roots. From the graph there is a small range of c where we will get two negative roots where 0< c < 1/4 and for all other values of c with two real roots we get that one is positive and the other is negative.
Let's now try to graph several of these at a time and see what varying the b value does to the roots of the equation. Let's choose the equations 0 = x^2 + bx +c where we allow b = -3,-2,-1,0,1,2,3.
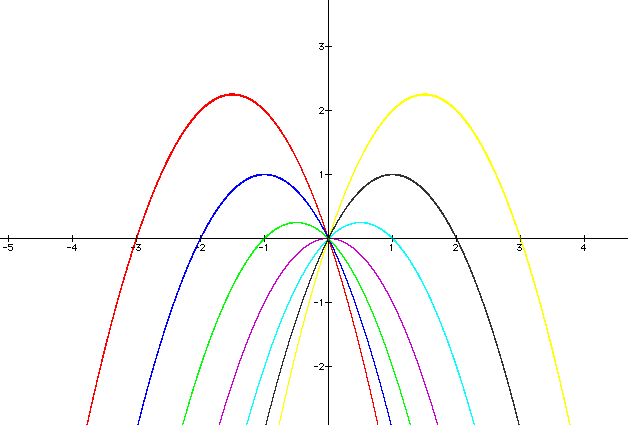
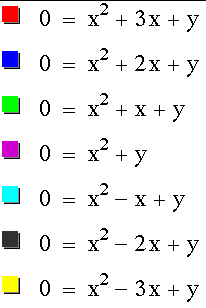
As you can see as the b value increases and decreases there are more c values for which we get two negative or two positive roots both because the c value of the vertex of the parabola is increasing and because the absolute value of the x value of the vertex of the parabola is increasing.
This new way of looking at roots for parabola's requires teaching students to understand and interpret a different kind of graph then the more standard way. It allows us to see visually how altering the b and c values changes the roots of the quadratic equation. Having students factor quadratics while also using this visual method might help them make a connection as to what a reasonable answer to the pure algebraic manipulation would be so that they can check algebraic work by using this graphical method, with the graph providing a more concrete frame of reference for the student.