Assignment 7
Constructing Two Tangent Circles to
a Line and a Circle
Overview: First,
I will discuss two different constructions of how to find two
tangent circles to a given line and a given circle. I will then
look at the locus of points of the centers of the two tangent
circle and look for interesting relationships. Finally, I will
use these two constructions to discuss some of the issues involved
in teaching mathematics and then demonstrate how these two constructions
apply to those issues by considering what we can take away from
each construction.
Construction 1: First,
we are given a line and a circle with a point P that lies on the
circle as shown below.
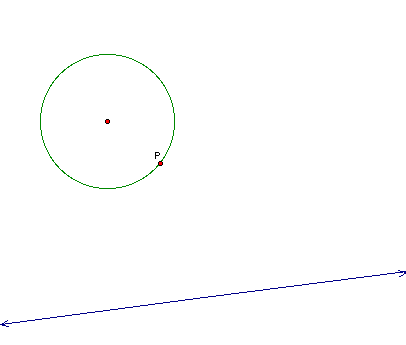 We need to find the
two tangent circles to the line and the given point on the circle.
We do this by first constructing a line through the center of
the circle perpendicular to the given line and a line through
the point P also perpendicular to the given line as seen below.
We need to find the
two tangent circles to the line and the given point on the circle.
We do this by first constructing a line through the center of
the circle perpendicular to the given line and a line through
the point P also perpendicular to the given line as seen below.
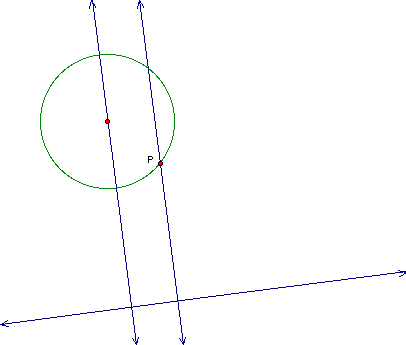 Next we draw a line
through the center of the circle and the given point P. The center
of the smaller tangent circle must lie along this line. Why?
Next we draw a line
through the center of the circle and the given point P. The center
of the smaller tangent circle must lie along this line. Why?
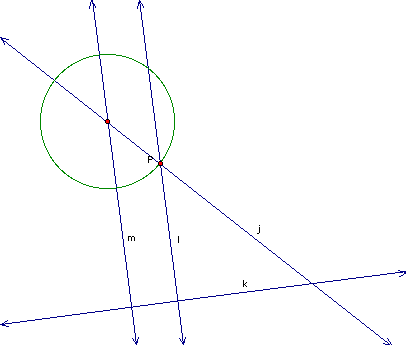 If we find the point
along line j such that the height from the given line to line
j is equal to the distance from point P along line j to this point
then we will have a circle that is tangent to the given circle
and the given line. Click here and hit the animate
button to see an animation. In this animation the center will
be at the point when PF = PG.
If we find the point
along line j such that the height from the given line to line
j is equal to the distance from point P along line j to this point
then we will have a circle that is tangent to the given circle
and the given line. Click here and hit the animate
button to see an animation. In this animation the center will
be at the point when PF = PG.
How do we find this point? Let's draw the portion
of line m between the circle and line k and the segment between
point P and line k and find the midpoint of each segment. Then
draw the line through the two midpoints, and this intersection
point is the center of the circle that is tangent to the given
circle and given line.
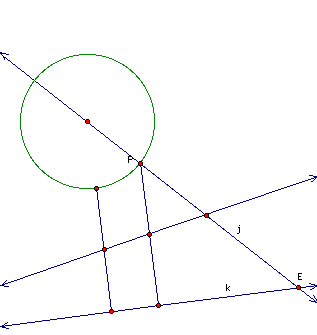 |
Now let's construct the
circle and see if we can find the second circle. |
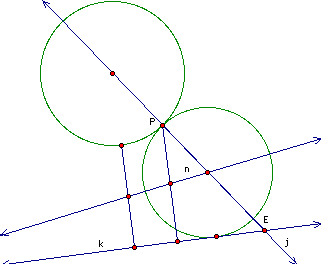 |
The second circle we can find by drawing a
perpendicular at the point where line k intersects line n. The
radius of the circle is then the distance from this perpendicular
to where it intersects line j.
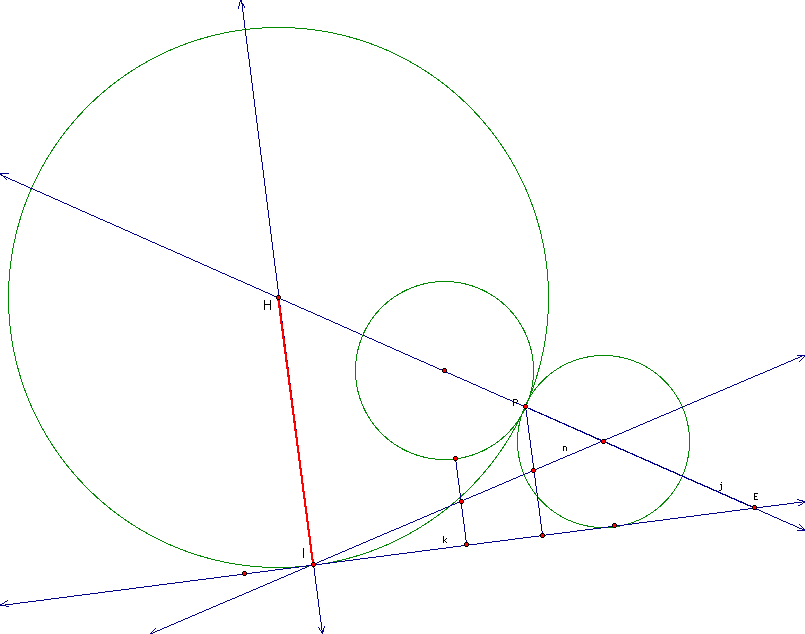 So HI is the radius
of the second tangent circle. Let's have a look at why this construction
gives us two tangent circles. As of yet, I have yet to figure
out why this construction works. I will post it when I figure
it out.
So HI is the radius
of the second tangent circle. Let's have a look at why this construction
gives us two tangent circles. As of yet, I have yet to figure
out why this construction works. I will post it when I figure
it out.
Construction 2: Let's
look at a slightly different construction of these tangent circles
for which I do understand the justification of the construction.
The construction begins the same way with a given circle and a
point P that lies on this circle and a given line. We first want
to draw a line through the center of the circle and the point
P as shown below.
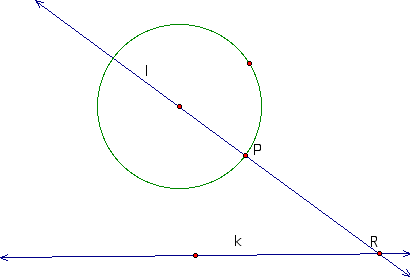 |
Now we draw
the tangent line to the circle at the point P. As shown to the
right. |
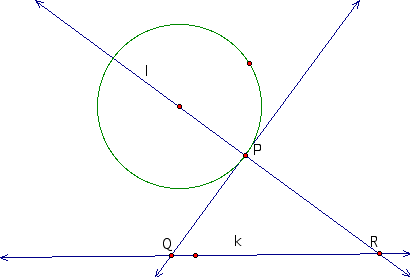 |
Now, if we draw the angle bisector of PQR this
should intersect line l at the center of the circle tangent to
the the given circle and the given line.
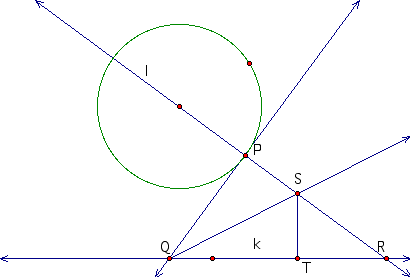 I have also drawn
in the segment that is perpendicular to line K from the point
S. We now have that triangle PQS is congruent to triangle TQS
by AAS or SAS. This means that PS is congruent to ST and therefore
we know that S is the center of the tangent circle with radius
length PS. If we bisect the supplementary angle to PQS we get
a second point of intersection along line l and this serves as
the center of our second tangent circle.
I have also drawn
in the segment that is perpendicular to line K from the point
S. We now have that triangle PQS is congruent to triangle TQS
by AAS or SAS. This means that PS is congruent to ST and therefore
we know that S is the center of the tangent circle with radius
length PS. If we bisect the supplementary angle to PQS we get
a second point of intersection along line l and this serves as
the center of our second tangent circle.
Locus of points for construction 1: Let's now take a look at the locus of points swept
out by the centers of the two circles. Can we make any guesses
before we use GSP to animate? We know that the center of the circle
is equidistant from the point of tangency on the circle and the
point of tangency on the line. Does this help? Let's look at the
results of the animation.

It looks like the top curve that is swept out
is a parabola. It is less clear what the bottom curve is but let's
go back to the definition of a parabola and see if it makes sense
that that is what we are getting. We know that the center of each
circle is equidistant from the point P of tangency on the circle
and the point of tangency with the given line. The definition
of a parabola is given a line and a fixed point not on that line
a parabola is the set of all points that are equidistant from
the point and the line. It looks convincing but there is one problem
with the definition--namely that the point P is not a fixed point.
In other words P is moving around the circle and the centers of
the circles are equidistant from a point that is moving. It appears
then that these may not be parabolas.
This, however, is an incorrect interpretation.
In fact, in this case our gut intuition is correct. These curves
are indeed parabolas. Why? If we take our fixed point to be the
center of the given circle and take a line parallel to the given
line but below it this point and line work as the fixed point
and given line as stated in the definition above.
What happens as we move the line to various
different places? Let's try by putting the line in the interior
of the circle.
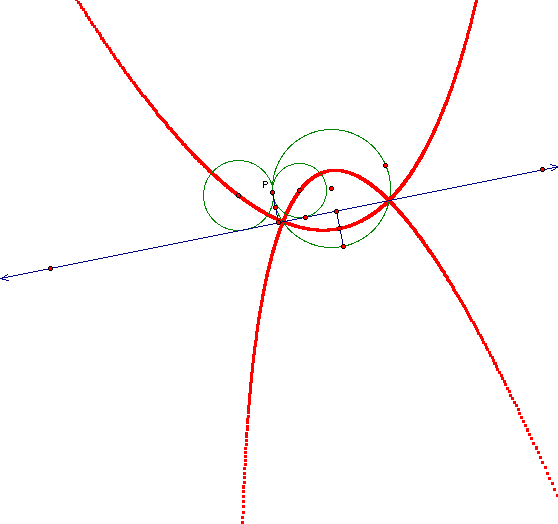
When we have the line inside the circle one
parabola opens up and the other opens down. Based on this evidence
can you guess what happens when the line is above the circle (I
will leave this as an investigation for the reader)? If
you want to investigate yourself click here and click on the animation
button.
In this construction are there any other interesting
geometric relationships? Let's focus on the segment perpendicular
segment that connects P to the given line. We know that the midpoint
of this segment is equidistant from point P and the point on the
given line as P moves around the circumference of the circle.
If we take the locus of the midpoints as P moves around the circle
can you think of what geometric shape this will trace out?
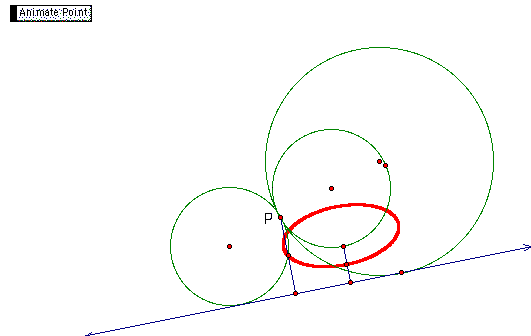
As we trace this midpoint, we get what I think
is an ellipse. To investigate this animation
yourself click here. I am not sure what the two focal points
would be so I will leave this as an unproved conjecture. What
relationship does this ellipse have to the two parabolas? Let's
again take a look at the GSP animation to find out.
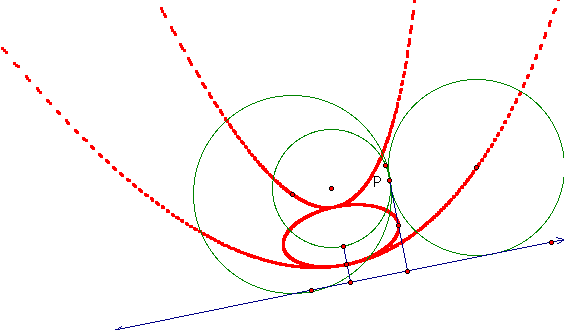
It is tangent to both of the parabolas which
the centers of the circles sweep out.
Locus of points for construction 2: The locus of points for the second construction gives
us the two parabolas but it doesn't give us this interesting relationship
between the ellipse and the two parabolas. Now let's think about
the advantages and disadvantages in the classroom of these two
constructions.
Looking at these two constructions from
a teacher standpoint: The second construction
is a bit more clean than the first. It requires less steps and
the justification of why it works can be easily seen (hopefully
by the teacher and also is easier to explain to students). One
of the difficulties of allowing students to arrive at solutions
of their own is that they may come up with solutions for which
you cannot readily justify but which work. Therefore, it is easy
to fall in to a pattern of too much directed guidance when solving
problems and not allowing your students to come up with creative
solutions to a problem. What is lost when you tell students how
to solve a problem rather than give them the skills to problem
solve themselves? Not only are students learning only through
repition often times interesting mathematics is missed when we
look for only one way to arrive at a mathematical solution. This
problem provides a perfect example as the second construction
doesn't allow us to see the relationship between the ellipse as
the two parabolas. In both constructions, the problem is answered.
It is valuable to allow students to see if they can come up with
a construction with the teachers guidance. Having several different
constructions provides the opportunity to discuss the strengths
and weaknesses of each. The strength of construction 1 is that
it allows us to further investigate mathematical relationships
that construction 2 does not allow. The strength of construction
2 is that it is easily justifiable and solves the problem efficiently.
Multiple solutions of a problem often bring these issues to the
floor and provide for great discussions in class.
Return to Main
Page
 We need to find the
two tangent circles to the line and the given point on the circle.
We do this by first constructing a line through the center of
the circle perpendicular to the given line and a line through
the point P also perpendicular to the given line as seen below.
We need to find the
two tangent circles to the line and the given point on the circle.
We do this by first constructing a line through the center of
the circle perpendicular to the given line and a line through
the point P also perpendicular to the given line as seen below. Next we draw a line
through the center of the circle and the given point P. The center
of the smaller tangent circle must lie along this line. Why?
Next we draw a line
through the center of the circle and the given point P. The center
of the smaller tangent circle must lie along this line. Why? If we find the point
along line j such that the height from the given line to line
j is equal to the distance from point P along line j to this point
then we will have a circle that is tangent to the given circle
and the given line.
If we find the point
along line j such that the height from the given line to line
j is equal to the distance from point P along line j to this point
then we will have a circle that is tangent to the given circle
and the given line. 

 So HI is the radius
of the second tangent circle. Let's have a look at why this construction
gives us two tangent circles. As of yet, I have yet to figure
out why this construction works. I will post it when I figure
it out.
So HI is the radius
of the second tangent circle. Let's have a look at why this construction
gives us two tangent circles. As of yet, I have yet to figure
out why this construction works. I will post it when I figure
it out.

 I have also drawn
in the segment that is perpendicular to line K from the point
S. We now have that triangle PQS is congruent to triangle TQS
by AAS or SAS. This means that PS is congruent to ST and therefore
we know that S is the center of the tangent circle with radius
length PS. If we bisect the supplementary angle to PQS we get
a second point of intersection along line l and this serves as
the center of our second tangent circle.
I have also drawn
in the segment that is perpendicular to line K from the point
S. We now have that triangle PQS is congruent to triangle TQS
by AAS or SAS. This means that PS is congruent to ST and therefore
we know that S is the center of the tangent circle with radius
length PS. If we bisect the supplementary angle to PQS we get
a second point of intersection along line l and this serves as
the center of our second tangent circle.


