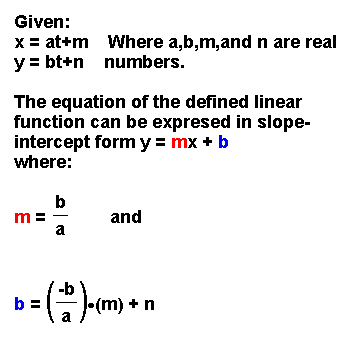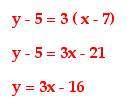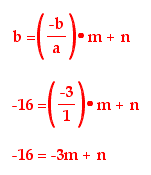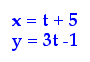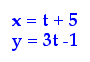Parametric Equations
and Linear Functions
In this assignment, we did explorations
using parametric equations. Parametric equations are written in
a 2 - vector form, and are a function of t, the time variable.
They are an alternative way to write various equations in terms
of time. As I was working through the explorations, I got interested
in the parametric equations that seemed to represent linear functions.
That is, instead of writing a linear equation in the form of y
= mx + b, expressing it using a set of parametric equations.
The main part of this investigation
began with exploring the equations  for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out.
for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out.
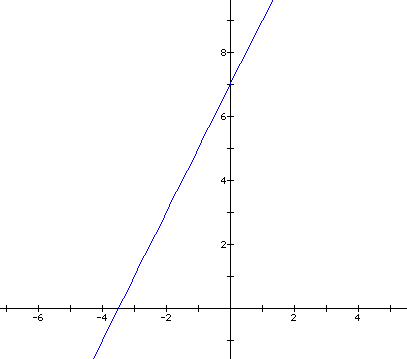
These equations appear to represent
a linear function. We can change the values of a,b and k to see
that any equations in this form will be linear graphs.
If we were to choose an appropriate
range for t, and then keep a and b constant while varying k, we
would see a family of related graphs. For example, for -100...t...100,
where a = 1 and b = 2, we can see the following graphs as k is
varied from the integers -3 to 3.
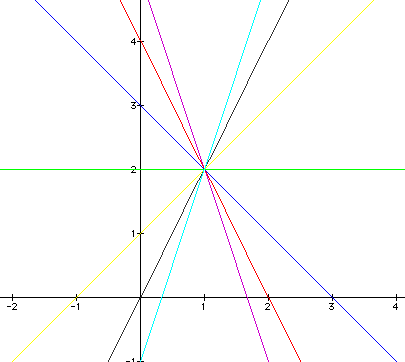
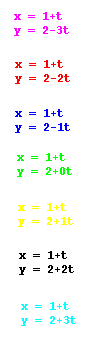
As you can see these parametric equations
represent a family of linear equations. In each case, the line
contains the point (1, 2), and the slope of the lines vary from
-3 to 3.
This exercise led me to think that there
must be some relationship between the parametric equation and
the resulting linear graph. The question of course is, what is
this relationship?
As I pondered this thought, I continued
to the next part of the assignment. In it we were told to graph
the equation 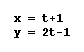 for an appropriate range for t.
I used -100...t...100. The graph of this equation was also linear,
as seen below.
for an appropriate range for t.
I used -100...t...100. The graph of this equation was also linear,
as seen below.
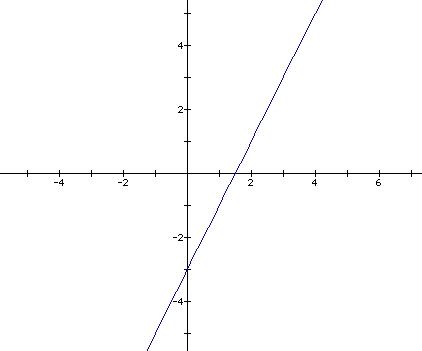 .
.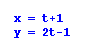
In need to find the relationship between
the two forms of the equations. To do this, I first decided to
find the slope and y intercept of the graphed line. In the above
case, the slope is 2/1, and the y intercept is -3. I remembered
from the last exploration that k controlled the slope of the line.
since k=2 in the y equation, perhaps that is where the slope comes
from. To check this, I decided to graph 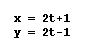 and
see how the two graphs compared.
and
see how the two graphs compared.
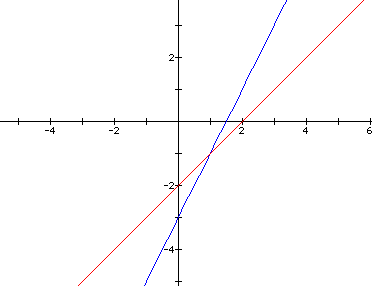
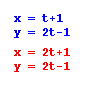
In looking art the graphs, we see that
thy both pass through (1, -1), However, the slope of the second
equation is now become 1/1 instead of 2/1. I'm inclined to believe
that the slope of the line will can be found by taking the ratio
of the coefficient of t in the y equation over the coefficient
of t in the x equation. Let's test this hypothesis. If my idea
is correct the graph of the equation 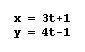 should
have a slope of 4/3. If we graph this equation as well, we can
see if we are correct.
should
have a slope of 4/3. If we graph this equation as well, we can
see if we are correct.
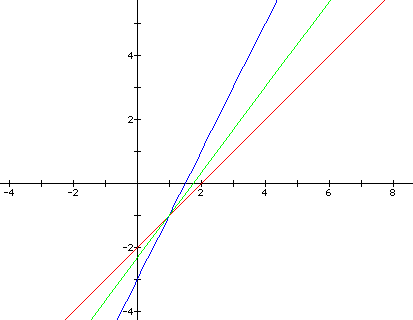
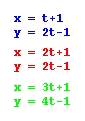
Looks like our hypothesis holds for
finding the slope of the line given the parametric equation. One
other thing we notice about these three lines is that they all
contain (1, -1). We know from our previous exploration that this
point is determined by the constant terms of the x and y equations.
In order to talk in more detail about the relationships found
here, let's define a general form for our set of parametric equations.
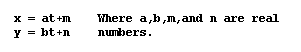
Now we can try to find a relationship
between the point that we know will always be on the line and
the y intercept of the line. I begin this task by keeping the
slope of the line a constant and manipulating the m and n variables.
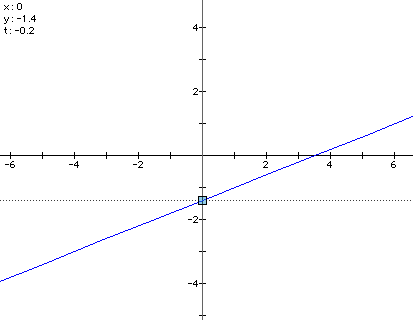
The first equation I want to look at is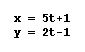 .
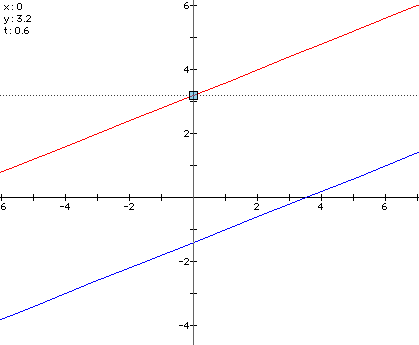
As you can see from the graph below, the y intercept of this line
is -1.4, and this value occurs when t = 0.2.
.
As you can see from the graph below, the y intercept of this line
is -1.4, and this value occurs when t = 0.2.
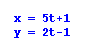
If we change our equation to 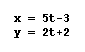 ,
we now see that the y intercept is 3.2 and the t value for this
is t = 0.6.
,
we now see that the y intercept is 3.2 and the t value for this
is t = 0.6.
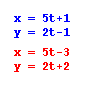
Let's look first at the value of t for
each of the equations. For 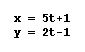 , we
see that t = -0.2. This value is related to the value of t if
the x equation were solved for zero. Let's check our idea for
the second equation
, we
see that t = -0.2. This value is related to the value of t if
the x equation were solved for zero. Let's check our idea for
the second equation 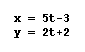 . Based on our calculated
values, we think t should equal 0.6, and we know from our graph
that it does. Excellent. Now, how does the value of t effect the
y intercept of the line. We know that the y intercept of a line
is the value for y when x = 0. since our y equation does not have
an x in it, I believe we can set the y equation equal to zero
and Solve for y. In order to do this, we first need to know the
value of t.
. Based on our calculated
values, we think t should equal 0.6, and we know from our graph
that it does. Excellent. Now, how does the value of t effect the
y intercept of the line. We know that the y intercept of a line
is the value for y when x = 0. since our y equation does not have
an x in it, I believe we can set the y equation equal to zero
and Solve for y. In order to do this, we first need to know the
value of t.
In 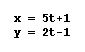 the
value of t = -0.2. this implies that y = 2(-0.2) - 1 , should
be the value of the y intercept. The expression above simplifies
to y = -1.4, which is the y intercept for that line.
the
value of t = -0.2. this implies that y = 2(-0.2) - 1 , should
be the value of the y intercept. The expression above simplifies
to y = -1.4, which is the y intercept for that line.
We can also check 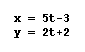 in
the same manner. We know t = 0.6, so the intercept should equal
2(0.6) + 2, which is 3.2, which is indeed the intercept for that
line.
in
the same manner. We know t = 0.6, so the intercept should equal
2(0.6) + 2, which is 3.2, which is indeed the intercept for that
line.
It appears that we have now established
formulas for the relationship between parametric and linear forms
of the same line. Let's state the relationships formally:
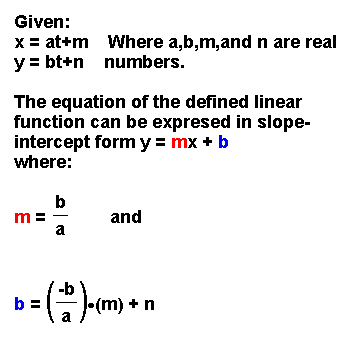
Realize that we get the y intercept
formula from solving x = at + m for t when x = 0,which is (-1/a)m, and substituting
it for t in the equation y = bt + n.
Now that we have discovered these formulas,
we can use them to go in the other direction. That is, given a
point on a line and the slope for that line, we can write parametric
equations to represent that linear function. For example,
if we wanted to find the parametric equations for the line passing
through (7,5), and having a slope of 3, we could do the following:
First, we would need to find the y intercept of this line,
so we use point slope form to do so:
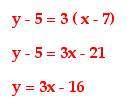
So, now we know that the y intercept of our line is -16. Since
m = 3, we can set 3 = b/a, and substituting -16 for the y intercept,
we can write:
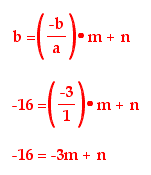
Since b/a has to be three, we choose b = 3 and a = 1. The
above equation tells us that -3m + n = -16. We know that there
are an infinite number of solutions to this equation, and any
one of them should work. We choose m = 5 and n = -1. This makes
our parametric equation for this line:
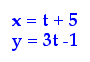
Let's graph these equations and make sure we have a line with
a slope of 3 and containing (7, 5).
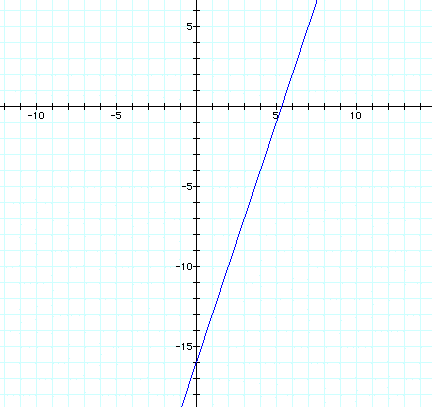
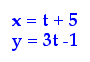
We do! (Celebrate if necessary!)
 for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out.
for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out. for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out.
for various values
of a, b and k. What type of graph will equations in this form
give us? Let's plug in some values for a, b and k and find out.
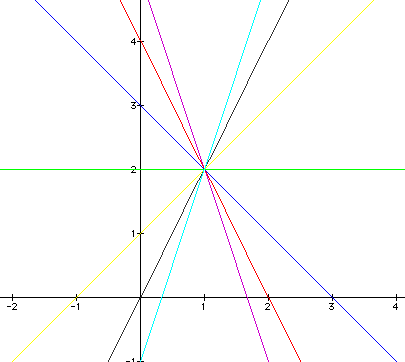
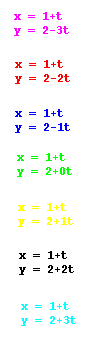
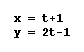 for an appropriate range for t.
I used -100...t...100. The graph of this equation was also linear,
as seen below.
for an appropriate range for t.
I used -100...t...100. The graph of this equation was also linear,
as seen below.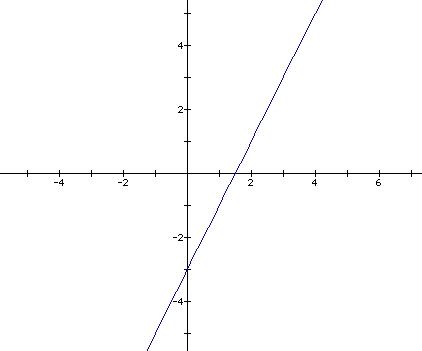 .
.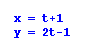
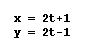 and
see how the two graphs compared.
and
see how the two graphs compared.
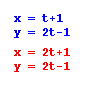
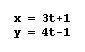 should
have a slope of 4/3. If we graph this equation as well, we can
see if we are correct.
should
have a slope of 4/3. If we graph this equation as well, we can
see if we are correct.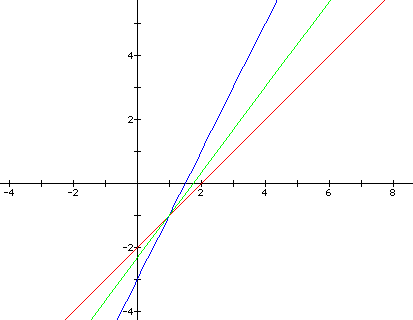
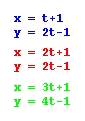
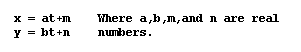
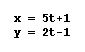 .
As you can see from the graph below, the y intercept of this line
is -1.4, and this value occurs when t = 0.2.
.
As you can see from the graph below, the y intercept of this line
is -1.4, and this value occurs when t = 0.2.
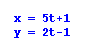
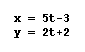 ,
we now see that the y intercept is 3.2 and the t value for this
is t = 0.6.
,
we now see that the y intercept is 3.2 and the t value for this
is t = 0.6.
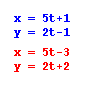
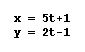 , we
see that t = -0.2. This value is related to the value of t if
the x equation were solved for zero. Let's check our idea for
the second equation
, we
see that t = -0.2. This value is related to the value of t if
the x equation were solved for zero. Let's check our idea for
the second equation 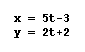 . Based on our calculated
values, we think t should equal 0.6, and we know from our graph
that it does. Excellent. Now, how does the value of t effect the
y intercept of the line. We know that the y intercept of a line
is the value for y when x = 0. since our y equation does not have
an x in it, I believe we can set the y equation equal to zero
and Solve for y. In order to do this, we first need to know the
value of t.
. Based on our calculated
values, we think t should equal 0.6, and we know from our graph
that it does. Excellent. Now, how does the value of t effect the
y intercept of the line. We know that the y intercept of a line
is the value for y when x = 0. since our y equation does not have
an x in it, I believe we can set the y equation equal to zero
and Solve for y. In order to do this, we first need to know the
value of t.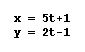 the
value of t = -0.2. this implies that y = 2(-0.2) - 1 , should
be the value of the y intercept. The expression above simplifies
to y = -1.4, which is the y intercept for that line.
the
value of t = -0.2. this implies that y = 2(-0.2) - 1 , should
be the value of the y intercept. The expression above simplifies
to y = -1.4, which is the y intercept for that line.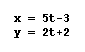 in
the same manner. We know t = 0.6, so the intercept should equal
2(0.6) + 2, which is 3.2, which is indeed the intercept for that
line.
in
the same manner. We know t = 0.6, so the intercept should equal
2(0.6) + 2, which is 3.2, which is indeed the intercept for that
line.