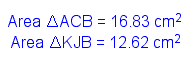Assignment 6
Explorations with GSP
"The Triangle of Medians"
The triangle of medians is the triangle
that can be constructed by using the three medians of a given
triangle. Say for instance that you were given triangle ABC
We know that the medians are the segments
drawn from each vertex to the midpoint of the opposite side.
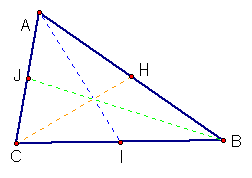
Using each of the median segments as
a radius of a circle, we can construct the yellow triangle below.
From point B, construct a circle with radius of AI. From point
J, construct a circle with radius CH. The intersection of these
two circles is point K, the third vertex of the triangle.
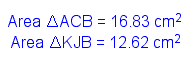
Using GSP to calculate the areas, and
then manipulating the triangles, we can establish that the ratio
of the yellow triangle is always 3/4 the area of the original
triangle. The question is why is this always true? Well good readers,
a proof shall follow...
A wise man once said, if you need to
prove something about the relationship between objects, it's easiest
to do so when they are a part of the same figure. Hence the reason
for constructing the triangle of medians within and around the
original triangle. A different, but equally wise man also said,
when you need to prove something geometrically, you almost always
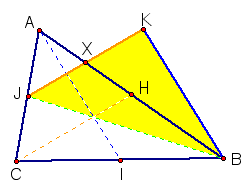
need to draw some construction lines. So we will begin by constructing
segments AK and JH parallel to segment CB, as well as KH, parallel
to AC. This will complete parallelogram AHJK.
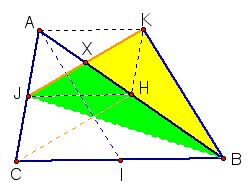
Since we know that the diagonals of
a parallelogram bisect each other, this makes X the midpoint of
segments AH and JK. With this, we can conclude that segment JX
is a median of of triangle AJH. Since a median of a triangle separates
the triangle into two triangles of equal area, we can state that
the area of triangle AJX is equal to the area of triangle JXH.
Or more importantly, that the area of triangle AJX is 1/2 the
measure of the area of triangle AJH.
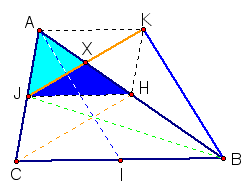
Since segment JH is, by construction,
a median of triangle AJB, we can use the same reasoning as above
to conclude that the area of triangle AJH is equal to the area
of triangle JHB, and therefore that the area of triangle AJH =
1/2 the area of triangle AJB. Since 1/2 x 1/2 = 1/4, we can conclude
that triangle AJX is 1/4 the area of triangle AJB, and that triangle
JXB is 3/4 the area of triangle AJB.
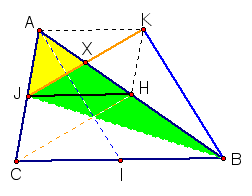
Now for some simple logic... If triangle
AJB is half of triangle ABC (the original triangle), and triangle
JXB is half of triangle JKB (the triangle of medians), AND, triangle
JXB is 3/4 the area of triangle AJB, we can finally conclude that
the triangle of medians is 3/4 the area of the original triangle.