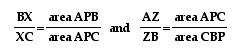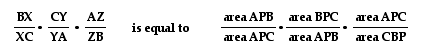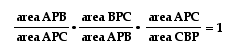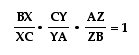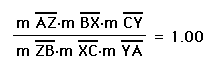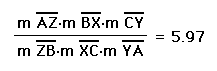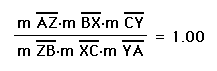Ceva's Theorem
In this assignment,
we are exploring the relationship between a given triangle ABC,
and any segments AX, BY, and CZ drawn from each respective vertex
of the triangle, to any point on the opposite side. I am excited
about this relationship, as it is something I have already discussed
and worked on. Namely, Ceva's Theorem. you may recall that in
my work with the Simson
line , I have
already explored and talked about this theorem. what follows below
is a proof of this.
Let's begin
by stating the theorem as Giovanni Ceva did back in 1678:

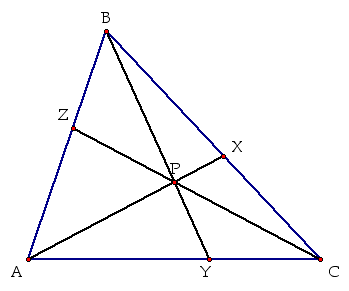
We start with
triangle ABC, with three cevians drawn concurrently through a
given point, in this case, point P.
The proof of this theorem
depends on the relationship between the area of a triangle, and
its base and altitude. We are going to describe triangles which
have the needed segments as bases in terms of their areas and
altitudes.
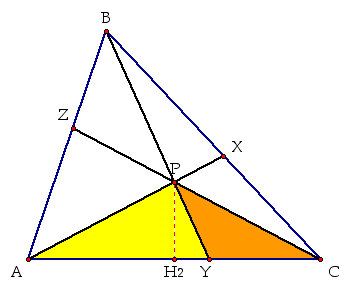
Let's begin with the
segments AY and YC, and their ratio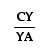 . Let's look at some triangles
that have these segments as bases, namely triangles ABY, and CBY.
. Let's look at some triangles
that have these segments as bases, namely triangles ABY, and CBY.

One thing you need to notice is that both triangles have the
same height (BH1). So when we express their areas in terms of
base and height, we see the following: 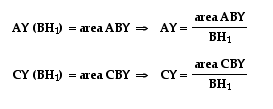
When we write these values as the ratio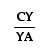 , we see that the altitudes drop
out leaving us with
, we see that the altitudes drop
out leaving us with 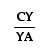 =
=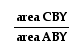 .
.
But, the above triangles
are not the only triangles with bases AY and YC. We can also use
triangles APY and CPY.
We can use the same
strategy as above to write . 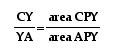 Now,
since we now know that
Now,
since we now know that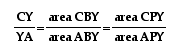 ,
,
and that areas are additive,
we can state that 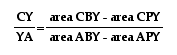 , or , using geometry's
area axiom
, or , using geometry's
area axiom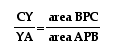 .
.
It is using the above
steps and applying them to the other ratios of Ceva's theorem,
that will allow us to rewrite the other two ratios as:
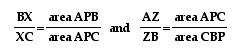
So, now, if
we replace each of the ratios in Ceva's original equation, with
the ones in terms of areas of the triangles, we see that: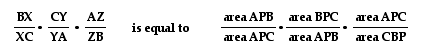
and that
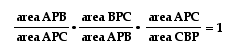
so, we can conclude
that
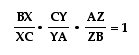
So, we now know that this relationship holds for any segments
drawn from the vertices to the opposite sides on the interior
of the triangle. The question is, can it be extended to segments
drawn from the vertices that intersect at a point on the exterior
of the triangle? Hmmmm, I wonder...
First, let's look at the theorem in the conditional form:

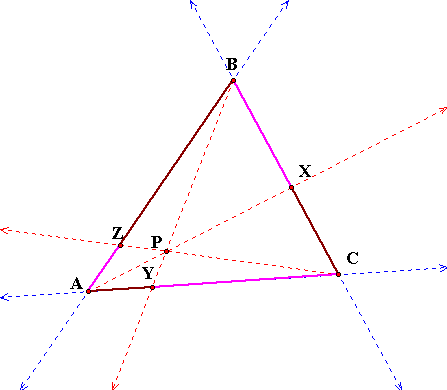
So, in GSP, I constructed
triangle ABC consisting of lines rather than segments. Next, I
chose a point P and drew rays from each of the vertices through
P. I constructed each of the segments: AZ, ZB, BX, XC, CY and
YA, and found their measures. I set up the ratio and found that
is was indeed equal to one.
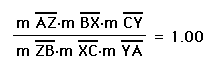
The question
is, will the ratio always hold for any location of P in the plane?
Well, in using the freshman
approach, I moved P around the plane and found that it would hold
for any point in the interior of the triangle. This came as no
surprise. however, there were several locations where the ratio
did not even exist, let alone equal one. One example of this is
below.
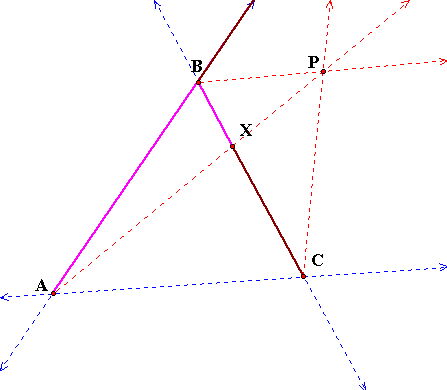
Why doesn't the ratio
exist in this location of P? Well, if you look at the ray BP,
you can see that it appears to be parallel to ray AC. I say that
this observation must be true. If BP were not parallel to AC,
then they would intersect. If they intersected, then segments
CY and AY would exist on line AC. They do not, which is why the
ratio does not exist in this particular location of P.
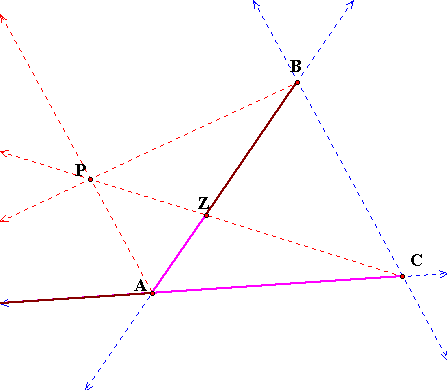
When P is in a location
such that AP is parallel to line BC, we will also not have a ratio
for the same reason. That is, that segments BX and XZ do not exist
on BC, hence they cannot be a part of the ratio.
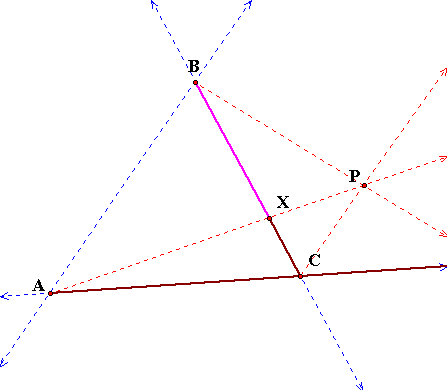
Above we see
the same problem. This time when P is on the line parallel to
AB and through C.
We can generalize
and say that Ceva's theorem will hold for any point P that does
not lie on the line drawn through a vertex of the triangle
and parallel to the opposite side.
Now we can look at the
converse of Ceva's theorem:
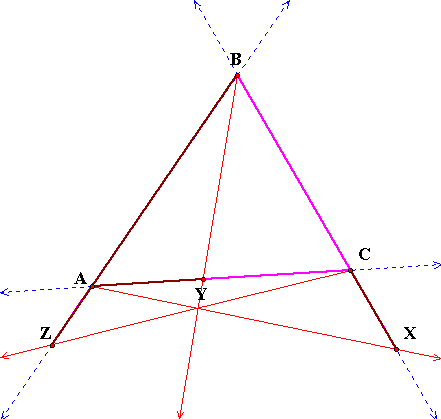
Once again, using GSP, I constructed
triangle ABC with lines in lieu of segments. Then, I constructed
points on each of those lines and drew rays from each vertex to
the point on the opposite side. Next, I constructed the segments:
AZ, ZB, BX, XC, CY,and YA and calculated their measures. I set
up the ratio I was looking for, and preceded to move the rays
around. As I did this I noticed the value of the ratio.
When the rays were not concurrent,
the ratio was not equal to one.
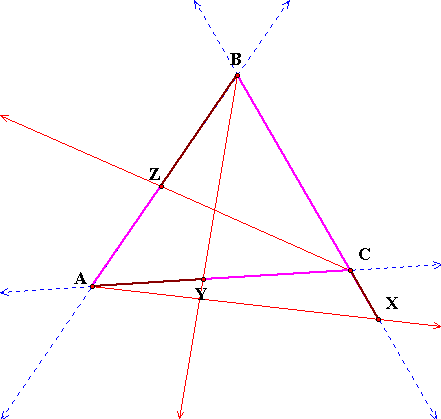
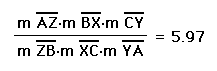
However, when the rays were
concurrent, the ratio did equal one.
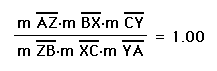
In order for the rays to be concurrent,
either all three rays must be within the interior of the triangle.
Or, only one ray can be in the interior of the triangle, and the
other two must be drawn on the interior of that vertex angle,
but outside the triangle.
To explore either of these GSP sketches,
click here to open my GSP
file. Page one of my file deals with
the given statement of Ceva's theorem, while page two employs
the converse.
The last thing to explore in this section deals with the triangle
that is formed by the feet of the cevians when P is in the interior
of the triangle. In the case below, triangle DEF. I will refer
to this triangle as the cevian triangle.
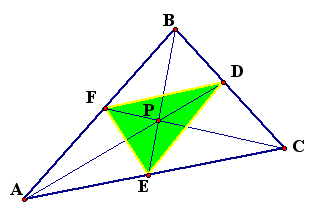
I looked at the ratio of the area of triangle ABC compared
with the area of triangle DEF, as P was moved within triangle
ABC. I found that the ratio of these two areas was always greater
than or equal to 4. The inevitable question of course is, WHY?
Let's begin with the case where the ratio is equal to four.
In order for this to happen, my theory is that P must be at the
centroid of the triangle . When P is located at the centroid of
triangle ABC, the cevian triangle DEF, is the medial triangle
of triangle ABC. The medial triangle is the triangle formed by
connecting the midpoints of the three sides of a given triangle.
If you wish, you can look at my web page on my exploration with
the medial triangle.
I first used GSP to see if indeed my idea made sense.
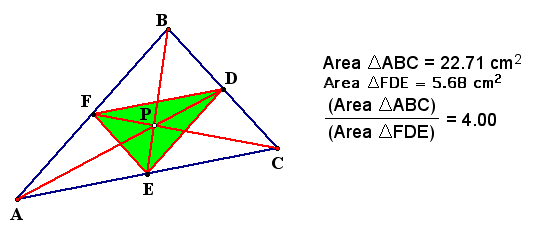
I constructed P as the centroid of triangle ABC, and then
drew the cevians through P. When I measured the area of the medial
triangle and compared it with the are of the original triangle,
it was indeed 4. The proof of this is as follows:
Since segment FD is drawn between two midpoints of a triangle,
we can conclude from the triangle mid segment theorem that it
is parallel to segment AC and equal to 1/2 of its length. Similarly,
we can state the same for segment pairs EF and CB, as well as
DE and BA. with each of these pairs in the ratio of 1:2, we can
state that triangle ABC is similar to triangle DEF by SSS similarity.
Since their perimeters are in the ratio of 1:2, we know that their
areas are in the ratio of the square of their perimeters, namely
1:4. So, we can conclude that when P is located at the centriod
of a triangle, that the ratio of the area of the original triangle
to the area of the cevian triangle is 4.
Now, our only question left to answer is, why is 4 the smallest
ratio value between the original triangle and the cevian triangle?
We can once again use GSP to explore the possibilities, and see
that the ratio never goes below four. But as we all know, this
does not count as a proof.
Using the information from above, we can also state that DEF
is congruent to each of the other smaller triangles, namely EDC,
AFE, and FBD by SSS congruency. This makes sense seeing that the
area of the original triangle is 4 times as large as the cevian
triangle. This will be the only time that this occurs. Let's prove
this by contradiction. Suppose there was another point P' such
that triangle DEF was similar to triangle ABC. If this was true,
we would know that all of the corresponding angles would be congruent.
We could use this information to establish parallel lines. Then
we would have a contradiction because in order for all of the
segments of DEF to be parallel to their corresponding sides of
ABC, D, E and F would have to be the midpoints of their respective
segments, which would imply that P' was at the centroid of the
triangle.
So, we can conclude that the ratio of the areas of the original
triangle to the area of the cevian triangle is always greater
than or equal to four.




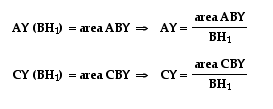
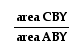 .
.
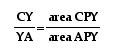 Now,
since we now know that
Now,
since we now know that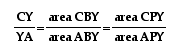 ,
,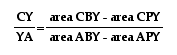 , or , using geometry's
area axiom
, or , using geometry's
area axiom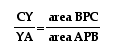 .
.