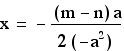Assignment 1, Question 3
Linear functions tangent
to the graph of their product
This investigation involves finding
two linear functions, f(x) and g(x) such that their product
h(x) = f(x).g(x)
is tangent to each of f(x) and g(x)
at two distinct points. Below is a summary of my investigation
of this problem.
I knew that in order to find the functions
I needed, that it was best to set up the equations involving variables
so I could check a lot of different combinations more easily.
I began by looking at the picture shown on the exploration question.
It looked to me as if the slopes of the two lines were 1 and -1,
so when I set up my first trial I decided to try the same thing.
I wrote two general linear forms: y= x+n, and y= -x+a. With these equations
in place, I also wrote their product as a function, namely y = (x+n)(-x+a).
I set a general range for n and set a = 1. I then discovered that
I could manipulate the value for n until the two lines were tangent
to the product of their functions. When a = 1, and n =0, the lines
were indeed tangent to the parabola.
But, I realized (eventually), that these couldn't be the only
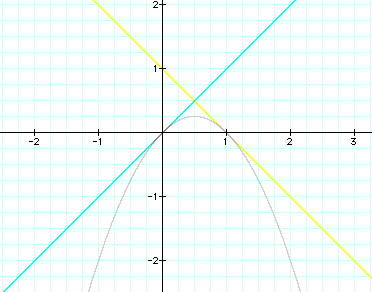
equations that would work for this particular problem. So, I changed
the value for a =2 and looked for another value of n that would
work.
This time, when a = 2, I found n = -1 would also give a solution.
I surmised that there could be infinite number of solutions
when the slopes of the lines were 1 and -1, the question was,
what was the pattern that they all fell into? I decided to look
for another pair.
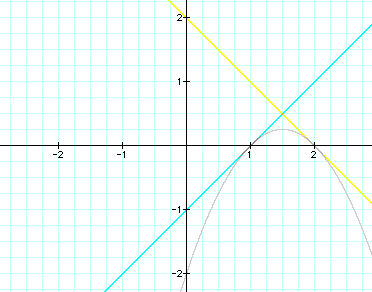
This time I set a = -1 and looked for a value of n. In order
to make both lines tangent, the n value needed to be 2.
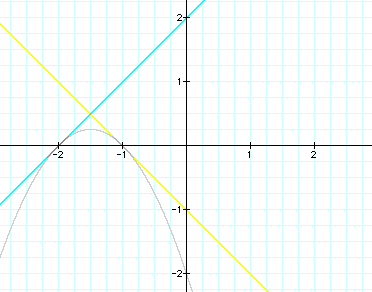
Now I had something to go on. I looked at my three sets of
equations for some relationship between them. I noticed that in
each case, the slopes were opposites and that the constants had
a sum of 1. I decided to test my hypothesis by writing two new
equations using my patterns and checking to see if the lines were
tangent to the parabola.
I used
y = x + 6
y = -x - 5
y = (x+6)(-x - 5)
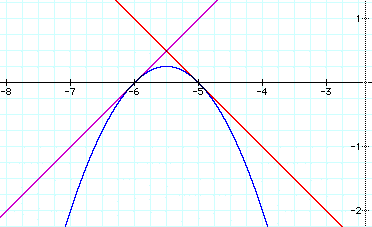
These were also solutions to the problem. So I decided that
in order to be a solution, the equations needed to be in the form
of
y = x +n
y = -x +a
y = (x+n)(-x+a), where n+a = 1
This is all well and good, but now I needed to do some exploring
with the slopes of the lines. Perhaps there was a pattern to them
as well.
Everything I had done to this point was with lines whose slopes
were 1 and -1. Were these the only slopes that this problem worked
for? It certainly didn't seem likely. So, next I tried to find
equations that would work when the slopes were not 1 and -1.
I first tried slopes of 1 and -3. I decided that the slopes
needed opposite signs at the very least. My choices of 1 and -3
were arbitrary. I graphed the equations y = x +n, y = -3x +a,
and y = (x+n)(-3x+a), with a value of a = 1. I figured it didn't
matter what value of a I started with. If these were to work in
the same way the slopes of 1 and -1 worked, I should be able to
find an n for any value of a. What I found instead, was that no
matter what value of n I used, I couldn't get both lines to be
tangent at the same time. You'll notice as the movie
plays, that each line will be tangent at some point, but whenever
one is tangent, the other clearly intercepts in two places.
So, I decided to try slopes that are opposites of each other,
like 2 and -2. I set up the general forms:
y = 2x +n
y = -2x+a
y = (2x+n)(-2x+a)
I started with a = 1 and looked for a value of n that would
make it true. I wondered if n = 0 would work in this case as well...
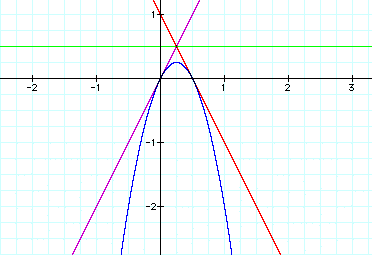
What do you know, it does! It could be that my condition of
a+n = 1 also holds true when the slopes are 2 and -2. I made another
guess for values of n and a and checked to see if it worked.
y = 2x + 7
y = -2x - 6
y = (2x+7)(-2x-6)
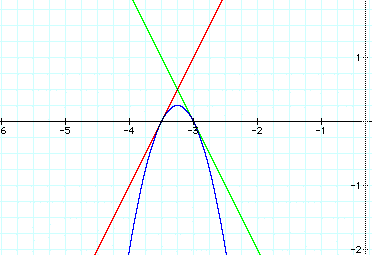
This is a solution as well. Perhaps it is time to make another
stab at a generalization. Suppose any equations in the form of
y = ax +n
y = -ax + m
y = (ax+n)(-ax+m), where m+n = 1
will be solutions to this problem. Time to try it out...
In order to test this new theory, I decided to establish a
set m and n, and vary the slopes with the variable a. This way,
I could check a number of different pairs of slopes at once. Check
out the resulting graphs
as I used the equations below and varied a from -10 to 10
y = ax+4
y = -ax - 3
y =(ax+4)(-ax - 3)
One of the things you should notice
as you view the graphs is that the intersections of the two linear
equations all lie on the line y =
1/2. Also worth noting is the fact
that each x coordinate of the lines intersection is the same x
coordinate of the vertex of the parabola. I suppose the next part
of this exploration should deal with why these things are true...
First lest deal with the fact that all
intersections lie along the line y = 1/2. We take our two general
linear equations and solve them as a system.
ax + y = m
-ax + y = n
Since the x's will drop out, add
the two equations
2y = m + n But,
m+n = 1, so...
2y = 1
y = 1/2
Now we need to explore why the x coordinate
of the intersection is always the same as the vertex of the parabola.
We solve the system again, but this
time we will solve the equations for x.
y = ax + n
y = -ax + m
Multiply the bottom equation by -1
to make the y's drop out.
0 = 2ax +(n - m) Add
-(n - m) to both sides
m - n = 2ax Divide
by 2a
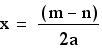
This is the x coordinate for the intersections
of this equation.
The parabola has the equation 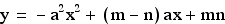
To find the x coordinate for its vertex,
we use the formula
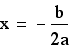
Substituting in we get...
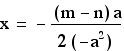
The negatives will cancel out, as well
as one factor of a, this leaves us with:
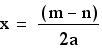
This shows that the values will always
be the same.