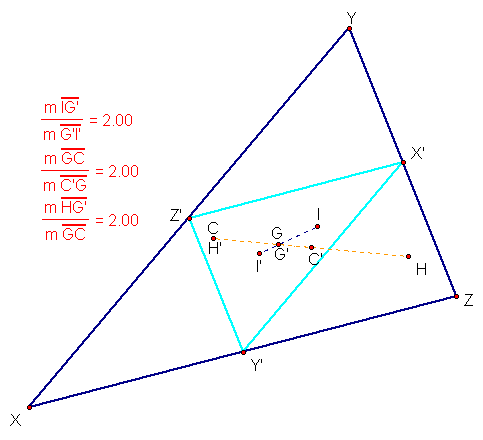Exploring Centers of Triangles
Within The Medial Triangle
Centers of a Triangle
Unlike a circle, which has only one
defined center, in any given triangle, there are several centers.
The centers are formed by the intersections of various lines within
the triangle.
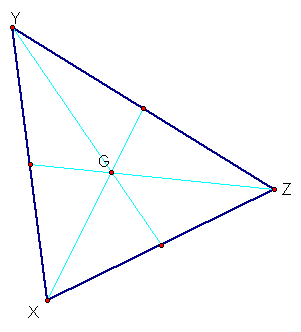
The centroid (G) of a triangle
is formed by the intersection of the three medians of the triangle.
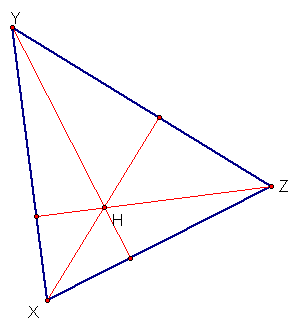
The orthocenter (H), is formed
by the intersection of the three altitudes of the triangle.
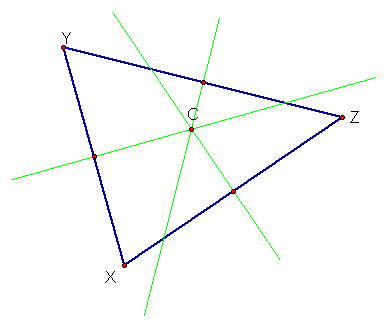
The circumcenter (C), is formed
by the intersections of the perpendicular bisector of each side
of the triangle.
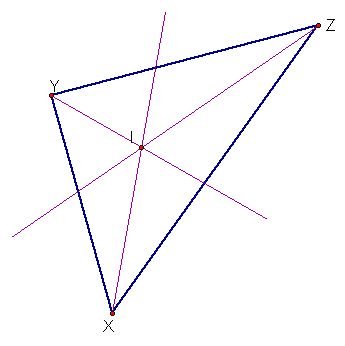
The incenter (I), is formed
from the intersection of the angle bisectors of each angle of
the triangle.
Each of these centers can be found within
any given triangle. When each center is found for the same triangle,
we can begin to see relationships between these four points.
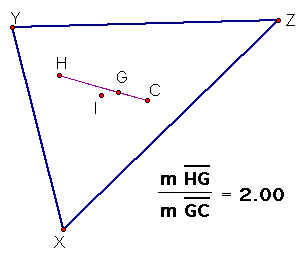
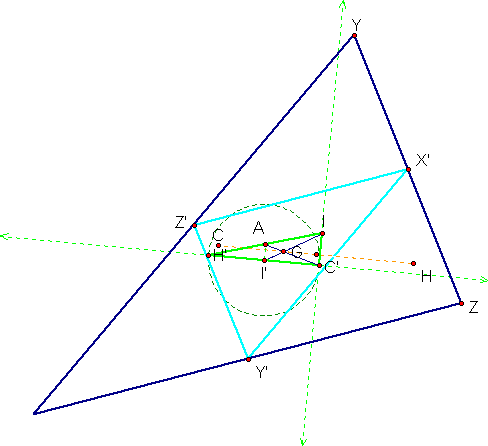
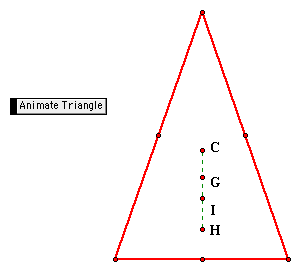
Notice first of all that points H, G,
and C are collinear. This will always be true for any size triangle.
Furthermore, G will always be between points H and C. As shown
by the calculation above, G divides segment HC so that the ratio
of HG : GC = 2:1. This relationship will also hold true for all
triangles. The line that contains this segment is known as the
Euler line. Choose this link to see the proof for the ratio of the Euler line.
You may notice that the point I is non
collinear to the other points in this particular case. However,
if the triangle is isoceles, all four points will be collinear.
Furthermore, if the triangle is equilateral, all four points will
be concurrent. Click on the picture below to open a GSP file showing
an animation of this idea.
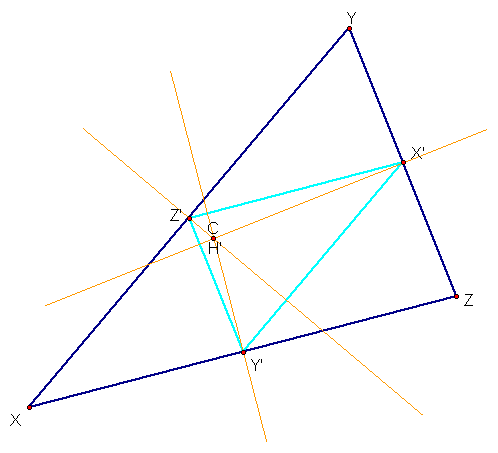
The Medial Triangle
Within any given triangle, one can construct
the medial triangle
by connecting the three midpoints of the original sides of the
triangle.
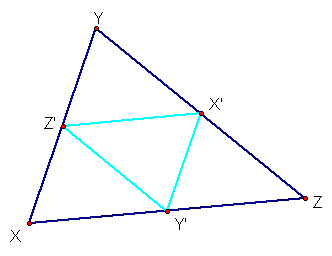
We can now locate each of the four centers
of this triangle as well. In finding C, G, H, and I for both the
original triangle and its medial triangle, we see this:
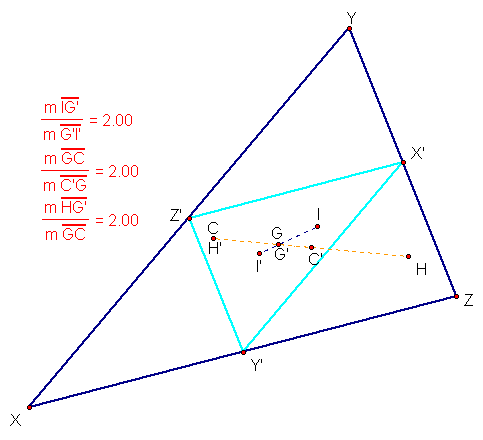
There are some interesting things happening
in this diagram that need to be discussed. The
first and most interesting fact is that some of the four points
in each triangle are the same. The second idea has to do with
the ratios of the segments formed by points I G and I'.
The circumcenter of the original triangle
(C) is the same point as the orthocenter of the medial triangle
(H'). Similarly, the centroid of both the original triangle (G),
as well as the medial triangle (G') are the same point.
It makes sense that the centroids are
both the same. The line that contains Z', the midpoint of side
XY, will also contain Z'',the midpoint of segment X'Y'. Likewise
the line that contains Y' will also contain Y'', the midpoint
of segment X'Z', and the line that contains X' will also contain
X'', the midpoint of segment Y'Z'. Since the three lines containing
X', Y', and Z', are the same lines as the ones containing X'',
Y'', and Z'', and those original three lines intersect at G, it
follows that the lines containing the other midpoints should do
so as well.
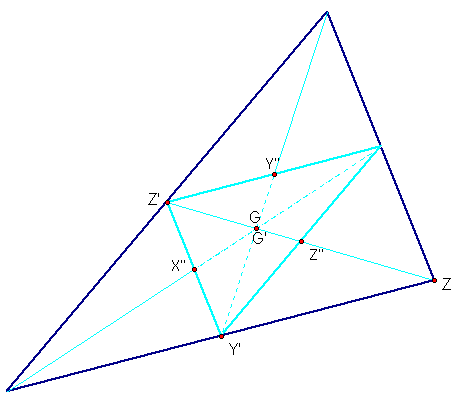
Now to discuss the reason for the coincidence
of H' and C. We know that the sides of the medial triangle are
parallel to the corresponding sides. That is that segment X'Z'
is parallel to segment ZX, and so on. Since this is true, any
line perpendicular to segment ZX will also be perpendicular to
X'Z'. Point C is the intersection of lines Y'C and X'C. Line Y'C
is perpendicular to XZ, so it is also perpendicular to Z'X'. since
this line is drawn through Y', this line is not only the perpendicular
bisector of XZ, it is also the altitude drawn to Z'X'. Following
this thought for each other perpendicular line, we find that the
three lines that intersect to form C, are the same lines drawn
to form H'.
The next thing to look into is the ratio
of segments within our original diagram.
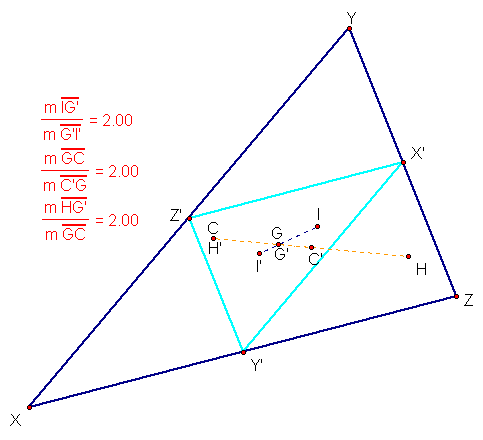
As you can see from the calculations
that have been done, three different pairs of segments are formed
in the ratio of 2:1. The fact that HG : GC is 2:1, and that H'G'
: G'C' is also 2:1 are not surprising as they are segments that
are a part of the Euler line for each of the two triangles. However,
the fact that the segments formed by the two incenters(I and I')
and the centriod (G/G') are also in the ratio of 2:1. This can
be explained very much in the same manner as we proved the ratios
of the Euler line. With the constructions shown below, we can
use a similar proof to the ones
above to show that triangles AGI' and
C'GI are similar by AA similarity, and since AI' : IC' = 2 : 1,
then I'G : GI is also 2:1.