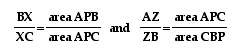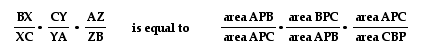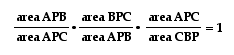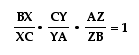Ceva's Theorem
A Proof
Let's begin
by stating the theorem as Giovanni Ceva did back in 1678:

We start with
triangle ABC, with three cevians drawn concurently through a given
point, in this case, point P.
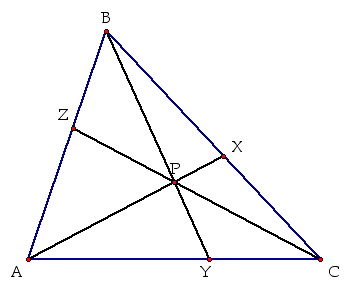
The proof of this theorem
depends on the relationship between the area of a triangle, and
its base and altitude. We are going to describe triangles which
have the needed segments as bases in terms of their areas and
altitudes.
Let's begin with the
segments AY and YC, and their ratio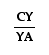 . Let's
look at some triangles that have these segments as bases, namely
triangles ABY, and CBY.
. Let's
look at some triangles that have these segments as bases, namely
triangles ABY, and CBY.
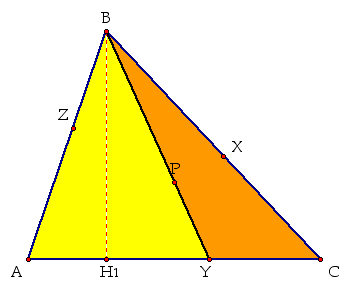
One thing you need to notice is that both triangles have the
same height (BH1). So when we express their areas in terms of
base and height, we see the following: 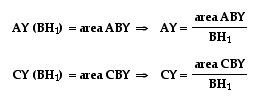
When we write these values as the ratio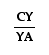 , we see that the
altitudes drop out leaving us with
, we see that the
altitudes drop out leaving us with 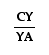 =
=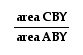 .
.
But, the above triangles
are not the only triangles with bases AY and YC. We can also use
triangles APY and CPY.
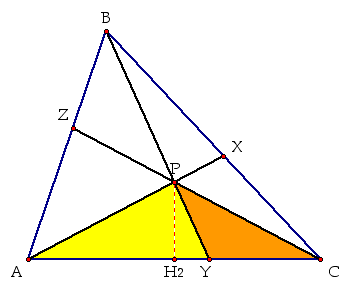
We can use the same
strategy as above to write 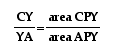 . Now,
since we now know that
. Now,
since we now know that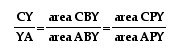 ,
,
and that areas are additive,
we can state that 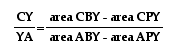 , or , using geometry's
area axiom
, or , using geometry's
area axiom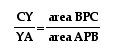 .
.
It is using the above
steps and applying them to the other ratios of Ceva's theorem,
that will allow us to rerwite the other two ratios as:
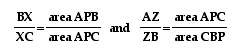
So, now, if we replace
each of the ratios in Ceva's original equation, with the ones
in term of areas of the triangles, we see that:
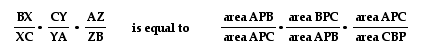
and that
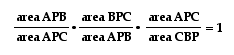
so, we can conclude
that
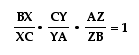




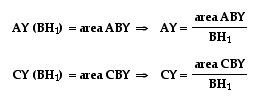
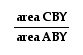 .
.
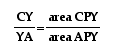 . Now,
since we now know that
. Now,
since we now know that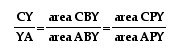 ,
, 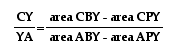 , or , using geometry's
area axiom
, or , using geometry's
area axiom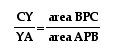 .
.