EMAT 6690: Essay One

Contextual Teaching and Learning

---

Problems with Cylindrical Tanks

In this essay, we want to consider the problem context of the storage of fluids in cylindrical tanks that have been installed laying on their side. What follows are two contextual situations whose common problem is that the DEPTH of the fluid is known, determine the volume.

First Situation

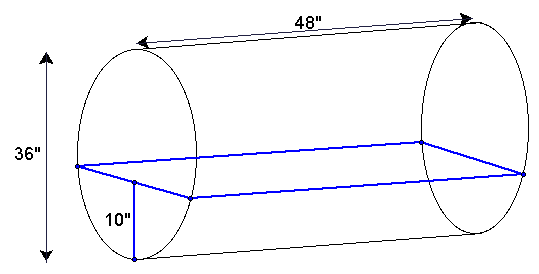
Suppose a person's furnace uses fuel oil stored in an underground tank. It is known that the tank is installed level on its side and that it is 36" in diameter and 48" long. Using a stick dipped through the fill tube, the person determined he had 10" of oil in the tank. He really does NOT want to know how to calculate the amount of oil. He knows from experience that it is February and he will need about 40 gallons of oil to finish the season. Will he have enough oil?

An estimate may suffice. For example, the surface of the oil is a rectangle 48" long and a little less than 18" wide. So the volume would be less than 48 x 36 x 10 cubic inches. This is the volume of rectangular parallelepiped. At 231 cubic inches per gallon, this gives an overestimate of 75 gallons. In fact if we approximate the oil in the tank by a triangular prism with altitude of 10", base of 36", and length of 48", its volume is half of this parallelepiped, or an estimated 37.5 gallons. That estimate is probably pretty close, but who would want to assure this guy that he has enough oil in the tank to finish out the winter on the basis of this estimate?

AND, could you tell this person how to make a calibrated dip stick - one with marks telling him how many gallons at each mark?

We will need to calculate the volume of the oil at each inch. In order to find the volume, we would have to find the area of the section covered by the oil at the end of the tank and then multiply by the length of the tank. But, how do you find the area of such a figure? Let's begin by examining the end view of the tank (in general so that we can do it for any size cylindrical tank in the future).

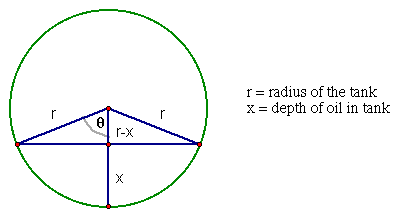
We begin by examining the sector formed by drawing radii to places where the oil meets the side of the tank. We can find the area of this sector and then subtract the area of the triangle that sits above the oil level.

Through Pythagorean relations, we can determine the length of the base of the triangle:

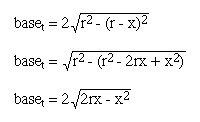
Thus, the area of the triangle is:

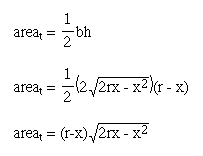
To find the area of the sector, we need the measure of the central angle that cuts it. We can find the measure of using inverse cosine.

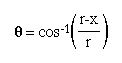
But, the central angle is . So, the area of the sector can be computed using the following relationship:

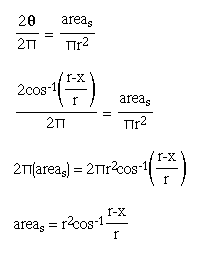
Now, we subtract the area of the triangle from the area of the sector to find the area of the oil at the end of the tank.

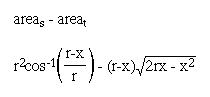
Multiplying by the length of the tank gives us the volume of the oil.

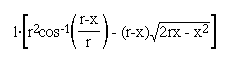
Since there are approximately 231 cubic inches in one gallon, we divide the volume by 231. Thus, the formula for the total gallons of oil in the tank is given by:

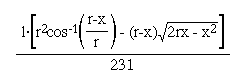
Now, we can plug in r = 18, x = 10, and l = 48 to get the number of gallons in the tank. We get 47.94 gallons.

Here is a graph of the volume function for the oil tank.

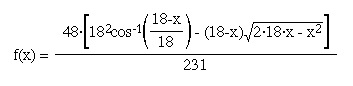
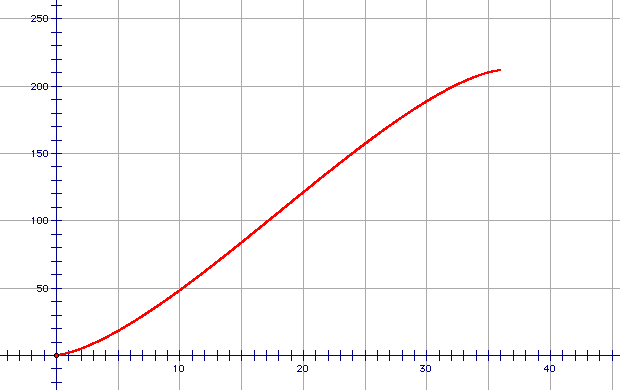
This graph confirms our estimate of the oil in the tank when the depth is 10". It also tells us that the maximum volume of oil in the tank is around 210 gallons. How would you calculate the maximum volume exactly? Just find the volume of the whole cylinder.

Here is a chart that we could use to make a calibrated dip stick for this tank.

Second Situation

The owner of a marine farm in southern Chile grows oysters and mussels in barrel shaped buoys that lie on their sides. Each buoy supports about one ton of product. He bases the maturity of his product on its weight. The heavier the product, the lower the buoy sits in the water. But, lifting the buoys out of the water for weighing would disturb the growth process. The area of the submerged buoy cross-section (a section of a circle) divided by the total area of the cross-section (a circle shape) and then multiplied by 1000 kg will give him a good approximation of what he has growing. Given the radius, r, and the perpendicular distance of the chord to the diameter, H, is there a way for this man to calculate the weight of his product without lifting the buoys out of the water?

While this is a completely different context than the oil tank, the concept is the same - here is an end view of the buoy.

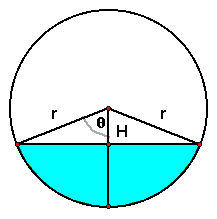
Through Pythagorean relations, we can determine the length of the base of the triangle:

Thus, the area of the triangle is:

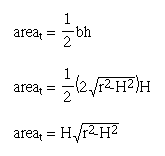
To find the area of the sector, we need the measure of the central angle that cuts it. We can find the measure of using inverse cosine.

But, the central angle is . So, the area of the sector can be computed using the following relationship:

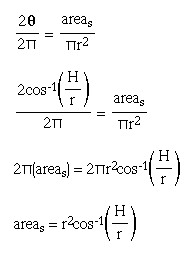
Now, we subtract the area of the triangle from the area of the sector to find the area of the submerged buoy cross section at the end of the tank.

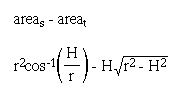
For an approximation of what he has growing, we divide this area by the total area of the cross section (a circle) and multiply by 1000 kg.

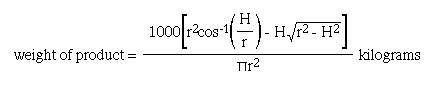
If the buoys support approximately one ton of product, that means they support about 907.2 kilograms at max capacity. Without knowing the dimensions of the buoys, we cannot graph the function...

In this essay, I have attempted to portray "real world" situations in which mathematics is not only useful, but essential. Do I have enough oil to make it through the winter? When are my mussels and oysters mature enough to harvest? While the mathematics involved is similar, the situations are completely different.

An idea for instruction: Discuss one situation with your students - perhaps the oil tank. Then, instruct them to do some research and find other contexts where cylindrical tanks are installed horizontally. I believe some of the most meaningful mathematics can be learned when one finds it himself/herself.

Some pictures...

fuel tank

fuel tank

cylindrical buoy

Return to Lauren's Home Page