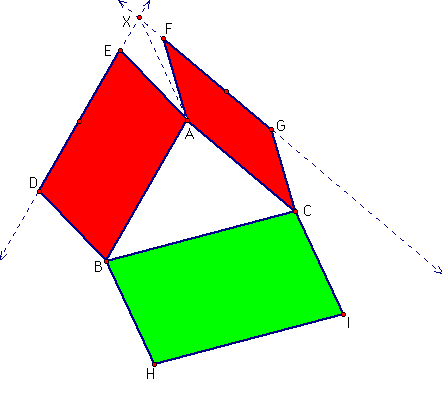
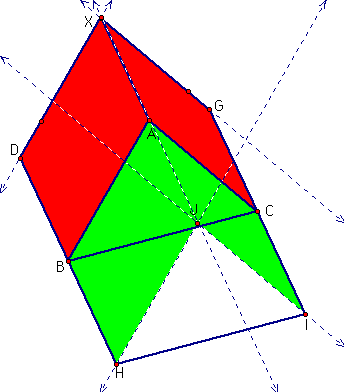
Take any triangle and construct arbitrary parallelograms on each side. Extend the two outer sides of the constructed parallelograms to where they meet. Use the segment of length d from this point to the near vertex of the triangle to define a length and direction for constructing a parallelogram on the third side. Show that the sum of the areas of the first two parallelograms (in red) is equal to the area of the third (in green).

The area of a parallelogram is found by multiplying the base times the height. It follows that I could move point E up to point X and still preserve the same area (because the height of the parallelogram has not been changed). Similarly, I could move point F up to point X, preserving the area of the original parallelogram.
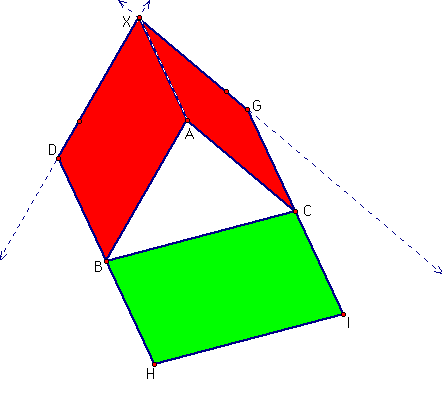
Now we construct a line parallel to AB through point H and line parallel to AC through point I.
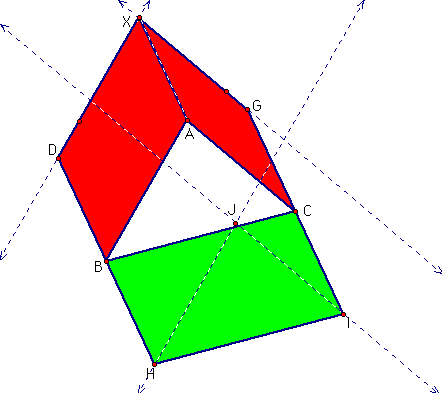

Return to Lauren's Home Page