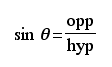
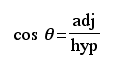
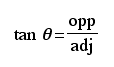
Key Concepts
There are six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent. Their abbreviations are sin, cos, tan, csc, sec, and cot respectively. Their ratios are formed by sides of a right triangle.
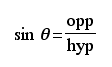
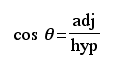
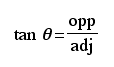
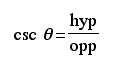
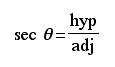
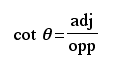
The abbreviations opp, adj, and hyp represent the three sides of a right triangle.
opp: the length of the side opposite theta
adj: length of the side adjacent to theta
hyp: length of the hypotenuse - the side opposite the right angle
GSP Activity
1. Begin with a segment.
2. Rotate the segment to create a 30 degree angle.
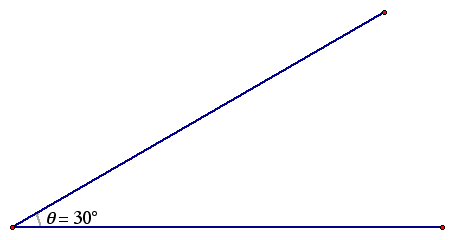
3. Construct a point on the segment and a perpendicular through that point.
4. Hide the extended lines so that you have right triangle ABC.
5. Using the Measure tool, find the lengths
of AB, BC, and AC. Then, find the following ratios: 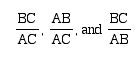
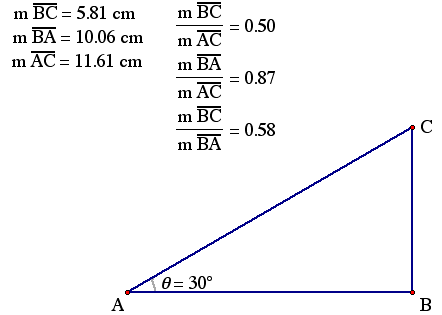
6. Highlight each of the calculated values and go to Tabulate (under the Graph menu). A table with all of the values should appear.
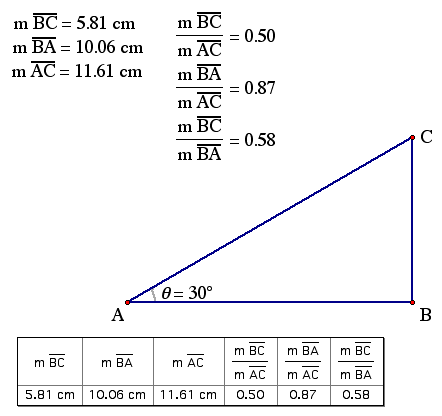
7. Move point B wherever you wish. You will notice that the values in the table change accordingly. . . To add new rows to the table, simply move point B and then double-click on the table. Add about 10 values to your table.
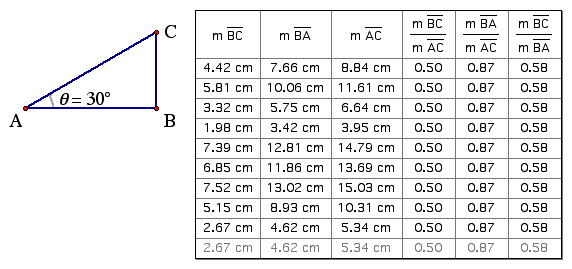
8. Can you make some observations about the ratios?
Click here to manipulate the above GSP file.
As you can see, the ratios stay the same regardless of the lengths of BC, AB, and AC. These are trigonometric ratios.

Q: If we examine the 60
degree angle of this right triangle, do you think the ratios will
be the same? Will they stay the same regardless of the lengths
of BC, AB, and AC?
Let's find out. . .
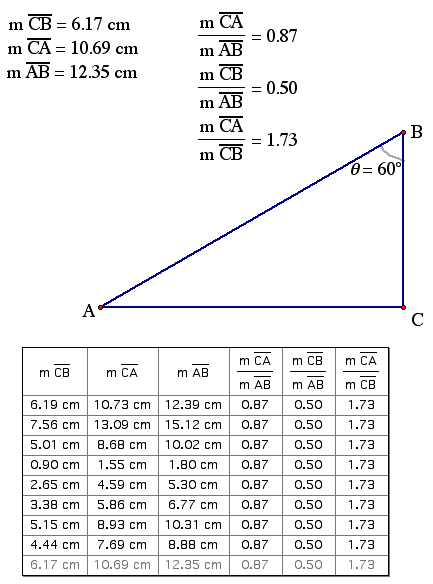
It appears that - like 30 degrees - the sin,
cos, and tan of 60 degrees remains the same no matter what! However,
the ratios are not equal to those of 30 degrees.
Let's take a look at a general angle theta and its trigonometric ratios.
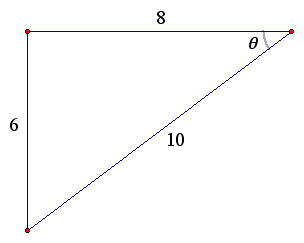
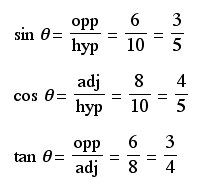
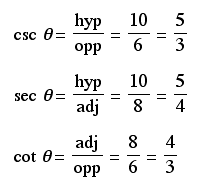
Special Right Triangles
1. The 30-60-90 triangle
We begin with an equilateral triangle.
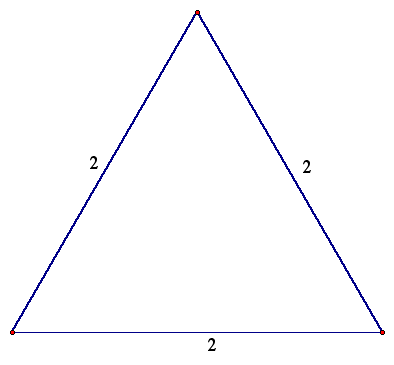
Then, we divide the triangle in half. We can find the length of the altitude using the Pythagorean Theorem.
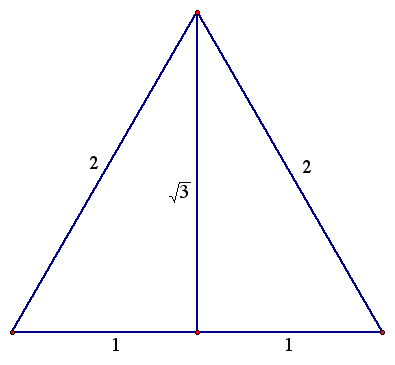
Now, by construction, each half of this triangle is a 30-60-90 triangle.
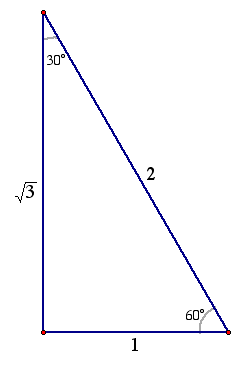
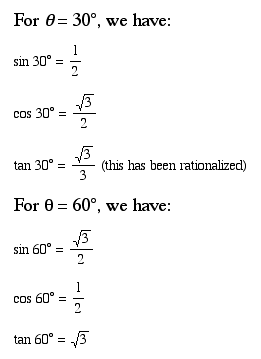
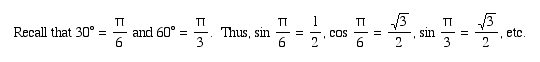
Q: What observations can you make about the relationship between the trigonometric ratios of 30 degrees and 60 degrees?
2. The 45-45-90 triangle
Begin with an isosceles right triangle (construct a segment, rotate it 90 degrees, connect the two remaining vertices.
Again, we can find the length of the hypotenuse using the Pythagorean Theorem.
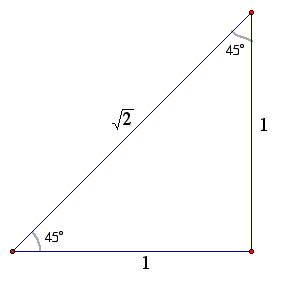
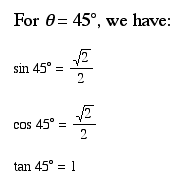
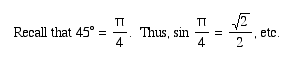
In this lesson, we have defined and discussed the six trigonometric ratios. We have also discussed the special triangles. 30-60-90, and 45-45-90.