Key Concepts
Let theta be an angle in standard position
with (x,y) a point on the terminal side of theta and![]()
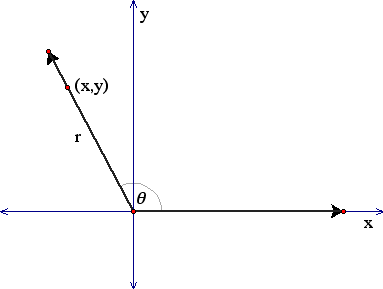
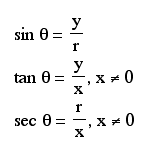
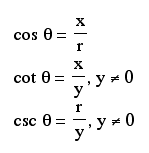
Click here for an overview of the six trigonometric functions.
The signs of the six trigonometric functions can be determined by examining the definitions of the functions given above.
For example, the sine of an angle is y/r. Since we know that r is always positive, the sign of sine depends on whether or not y > 0...
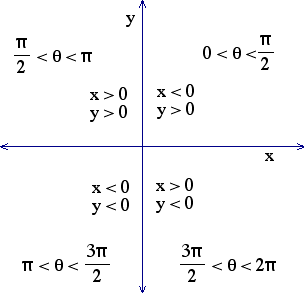
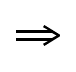
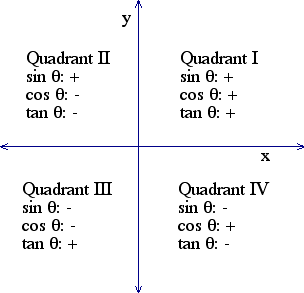
reference angle: If theta is an angle in standard position, its reference angle is the acute angle formed by the terminal side of theta and the horizontal axis

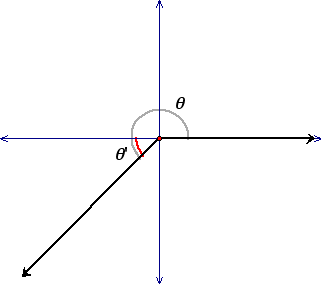
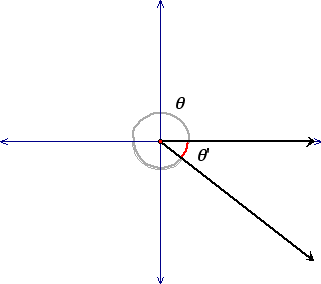
Click here for some interactive practice on estimating an angle's value based on its sine value.
Click here for some interactive practice on estimating an angle's value based on its cosine value.
We can use the information above to calculate trigonometric functions of any angle. First, we determine the measure of the reference angle. Second, we find the sign of the function. We can use reference angles to determine the exact trigonometric values of the most common angles.
| |
|
|
|
|
|
|
|
| |
|
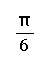 |
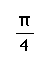 |
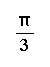 |
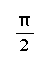 |
|
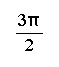 |
| |
|
|
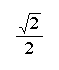 |
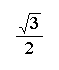 |
|
|
|
| |
|
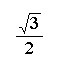 |
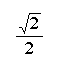 |
|
|
|
|
| |
|
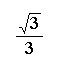 |
|
|
Undefined | |
Undefined |
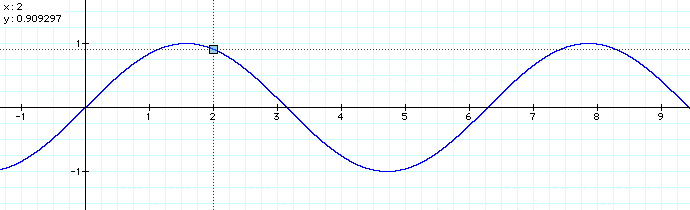
In this lesson, we have talked about calculating trigonometric values for the "special" angles - 30, 45, 60, 90, 180, and 360. The trigonometric values for other angles can be computed on a calculator (be sure you are in the correct mode - radian or degree), or estimated on a graph.
For example, suppose we wanted to estimate the value of sin at 2 radians. Here is a graph of the function (in radian mode) with a trace at x = 2. So, sine of 2 radians is approximately 0.909.