Predicting
the Temperature of Cooled Water
(or not...)
By: Lauren
Wright and Andy Tyminski
In this experiment, we took a pot of
boiled water and measured its initial temperature (time t = 0)
and then recorded temperature readings for the next 30 minutes.
You would think that this would be an easy task for two graduate
students...
After measuring the temperatures, we
entered them on a spreadsheet and ATTEMPTED to use Newton's Law
of Cooling to model the data and predict the temperature of the
water after 45 minutes, 60 minutes, or 300 minutes.
First, we will show you the data that
we collected with a room temperature of 74 degrees Fahrenheit.
| Minute |
Temperature |
Minute |
Temperature |
Minute |
Temperature |
| 0 |
212 |
|
|
|
|
| 1 |
204 |
11 |
155 |
21 |
136 |
| 2 |
192 |
12 |
153 |
22 |
135 |
| 3 |
186 |
13 |
151 |
23 |
134 |
| 4 |
180 |
14 |
149 |
24 |
132 |
| 5 |
175 |
15 |
147 |
25 |
131 |
| 6 |
171 |
16 |
145 |
26 |
130 |
| 7 |
168 |
17 |
143 |
27 |
129 |
| 8 |
164 |
18 |
142 |
28 |
128 |
| 9 |
162 |
19 |
139 |
29 |
127 |
| 10 |
159 |
20 |
139 |
30 |
125 |
The formula for Newton's Law of Cooling
is:
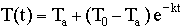with t = time in minutes, 
=
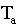temperature of the air, 
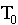= initial temperature,
and k = experimental constant.
First, we set out finding what our
k would be. We did this by calculating the value of k at five
different data points, namely T(6), T(11), T(19), T(26), and T(29).
Then, we took the average of those five k values to get an estimate
of our experimental constant.
The k that we used in Newton's formula
is k = 0.042901.
Here is a table of the values that
were returned.
| Minute |
Temperature |
Minute |
Temperature |
Minute |
Temperature |
| 0 |
212 |
|
|
|
|
| 1 |
206.204859462488 |
11 |
160.085646064217 |
21 |
130.05496264225 |
| 2 |
200.653078735481 |
12 |
156.470585069981 |
22 |
127.701003320969 |
| 3 |
195.334438222578 |
13 |
153.007334122942 |
23 |
125.445895630749 |
| 4 |
190.239147486782 |
14 |
149.68951814659 |
24 |
123.285488418732 |
| 5 |
185.357827228474 |
15 |
146.511029777924 |
25 |
121.215804854627 |
| 6 |
180.681492020207 |
16 |
143.46601812515 |
26 |
119.233035110248 |
| 7 |
176.201533766522 |
17 |
140.548877997494 |
27 |
117.333529346465 |
| 8 |
171.909705858361 |
18 |
137.754239587282 |
28 |
115.51379099466 |
| 9 |
167.798107992885 |
19 |
135.076958585322 |
29 |
113.77047032032 |
| 10 |
163.859171630773 |
20 |
132.512106711368 |
30 |
112.10035825692 |
As you can see, these values differ
greatly from what we recorded. Here is a graph of the two sets
of data.
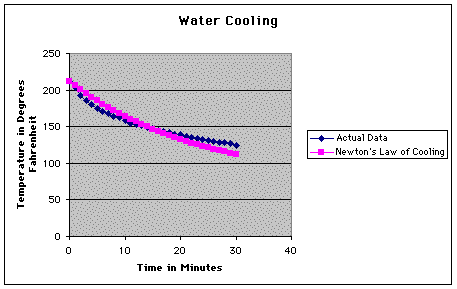
So, the next step in our experiment
was to see exactly how bad the error was.
We took the square of the difference
for each time, summed the squares, and divided by the number of
data points. This gave us an average error of approximately 60.3
degrees. For illustration, take a look at the graph of the residuals...
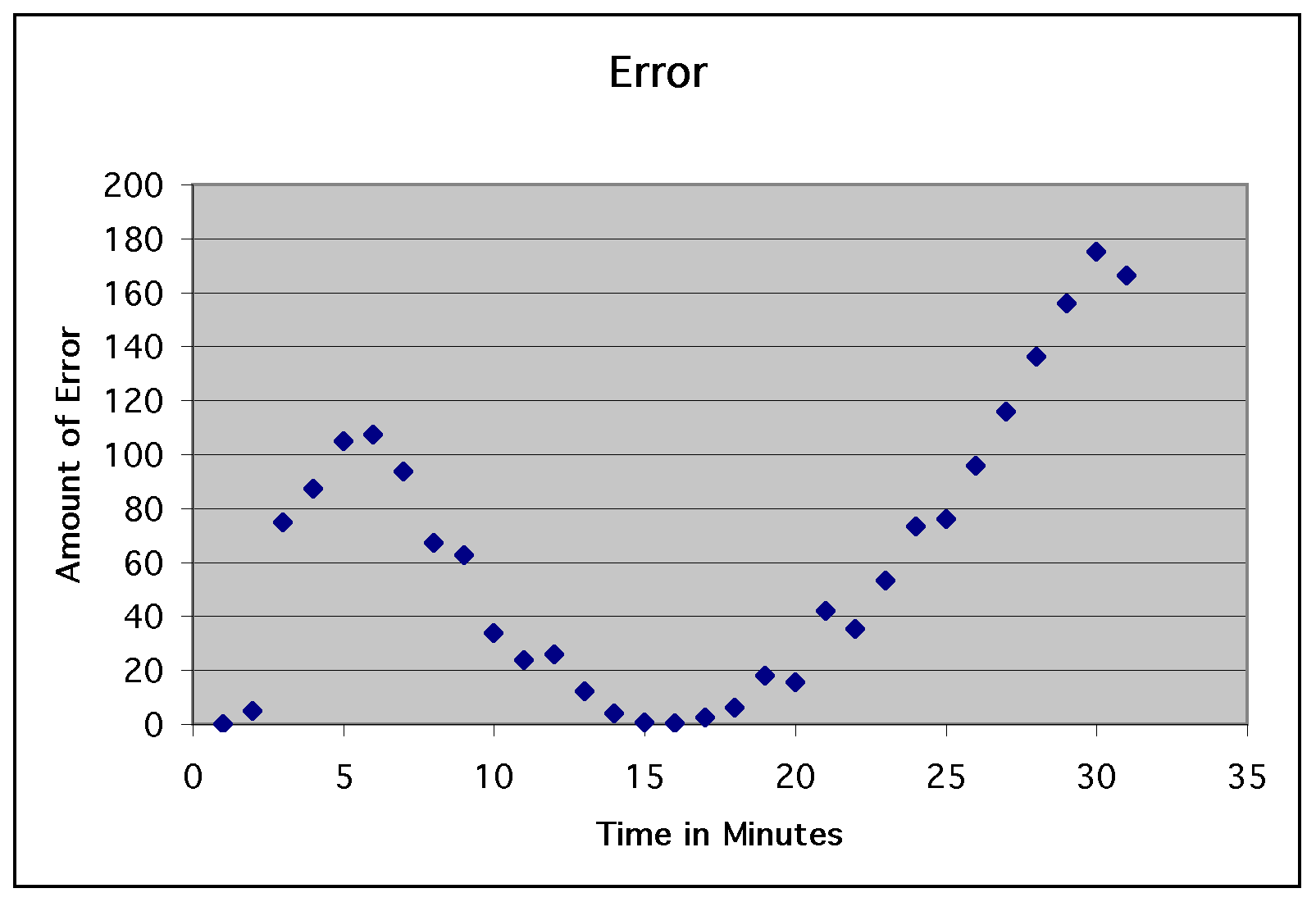So, this experiment was a complete
disaster using Newton's Law of Cooling. We could attribute this
to many factors - a faulty thermometer or human error are the
most likely causes (I mean, ANDY was in charge of reading
the thermometer. So, anything is possible.)
Return