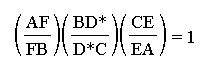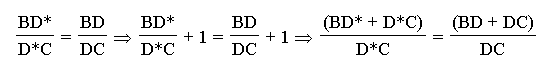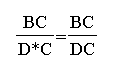Final
Assignment: Ceva's Theorem
by: Lauren
Wright
For this assignment, we consider any
triangle ABC. Select a point P inside the triangle and draw lines
AP, BP, and CP extended to their intersections with the opposite
sides in points D, E, and F respectively.
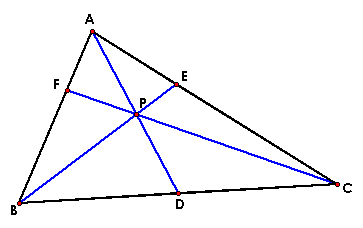 Then, we explore (AF)(BD)(CE) and (FB)(DC)(EA)
for various triangles and various locations of P.
Then, we explore (AF)(BD)(CE) and (FB)(DC)(EA)
for various triangles and various locations of P.
After exploring this in GSP, I came
to the conclusion that (AF)(BD)(CE) = (FB)(DC)(EA) whenever P
is inside the triangle. Or, more simply stated, we have:
 This is Ceva's Theorem, which states:
In a triangle ABC, three lines AD,
BE and CF intersect at a single point P if and only if
This is Ceva's Theorem, which states:
In a triangle ABC, three lines AD,
BE and CF intersect at a single point P if and only if
 (The lines that meet at a point are
said to be concurrent.)
(The lines that meet at a point are
said to be concurrent.)
Now for a proof...
Extend the lines CF and BE beyond the triangle
until they meet GH, the line through A parallel to BC.
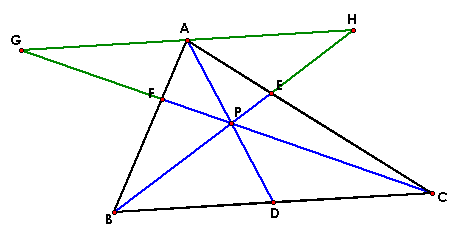
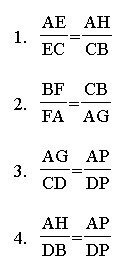
There are several pairs of similar triangles:
AHE and CBE, AFG and CBF, AGP and CDP, BDP and AHP. From these
and in that order we derive the following proportions:
from the last two we conclude that
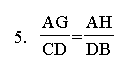 .
.
Therefore,
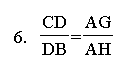 .
.
Multiplying #1, #2, and #6 together, we get:
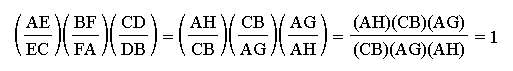
Therefore, if the lines AD, BE and CF intersect
at a single point P, the identity  does
hold. Which is to say that the fact of the three lines intersecting
at one point is sufficient for the condition
does
hold. Which is to say that the fact of the three lines intersecting
at one point is sufficient for the condition  to hold.
to hold.
Let us now prove that it's also
necessary. This would constitute the second part of the theorem.
In other words, let us prove that if  holds
then AD, BE, CF are concurrent.
holds
then AD, BE, CF are concurrent.
Let's assume that P is the point of intersection
of BE and CF and draw the line AP until its intersection with
BC at a point D*. Then, from the just proven part of the theorem
it follows that
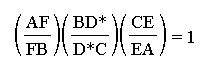
And it's given that

Combining these two, we get the following:
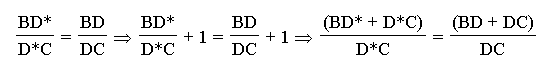
Therefore,
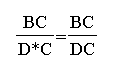
which implies D*C=DC. Or, D* and D are one
and the same point.
Click here
to see the website that assisted me in this proof.
This result can be generalized to (using lines rather than segments
to construct ABC) so that point P can be outside the triangle.
Click here for a working GSP sketch.
For the last exploration, we will look
at the ratio of the areas of triangle ABC and triangle DEF when
P is inside triangle ABC.
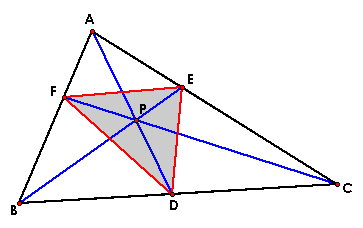 After building and exploring this triangle,
I found that the ratio of the areas is always greater than or
equal to 4. First, I want to look at the case when the ratio is
equal to 4.
After building and exploring this triangle,
I found that the ratio of the areas is always greater than or
equal to 4. First, I want to look at the case when the ratio is
equal to 4.
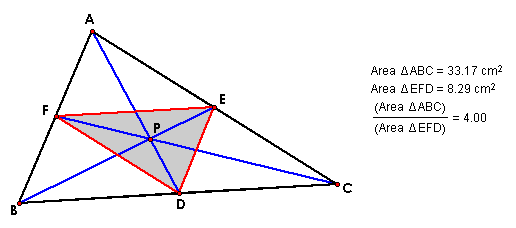 I noticed that D, E, and F appear to
be the midpoints of the sides of ABC when the ratio is equal to
4. I decided that this must mean that the ratio is equal to 4
when P is the centroid of ABC. That means that DEF is the medial
triangle. I know that the medial triangle is exactly one fourth
of the original triangle, so this makes sense for me. Now, if
P is not the centroid, why is the ratio of the areas going to
be greater than 4?
Well, I know that the medial triangle
is the largest triangle that can be formed inside the original
triangle, so the ratio of 4 must be the smallest that the ratio
of ABC to DEF can be - or greater than or equal to 4!
I noticed that D, E, and F appear to
be the midpoints of the sides of ABC when the ratio is equal to
4. I decided that this must mean that the ratio is equal to 4
when P is the centroid of ABC. That means that DEF is the medial
triangle. I know that the medial triangle is exactly one fourth
of the original triangle, so this makes sense for me. Now, if
P is not the centroid, why is the ratio of the areas going to
be greater than 4?
Well, I know that the medial triangle
is the largest triangle that can be formed inside the original
triangle, so the ratio of 4 must be the smallest that the ratio
of ABC to DEF can be - or greater than or equal to 4!
Return






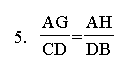 .
.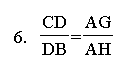 .
.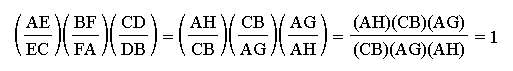
 does
hold. Which is to say that the fact of the three lines intersecting
at one point is sufficient for the condition
does
hold. Which is to say that the fact of the three lines intersecting
at one point is sufficient for the condition  to hold.
to hold. holds
then AD, BE, CF are concurrent.
holds
then AD, BE, CF are concurrent.