Explorations with
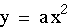by: Lauren Wright
In this assignment, we explore the
effects of changing a on the graph of
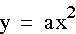
First, let's examine this graph for a
> 0.
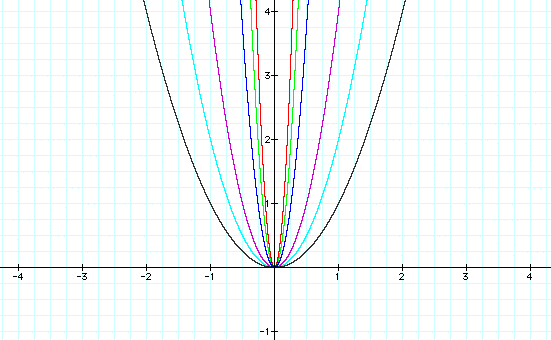Looking at these graphs we can draw
the conclusion that the bigger a is (or the further a
is from zero), the more contracted the parabola becomes.
Now, let's look at the graph for a <
0.
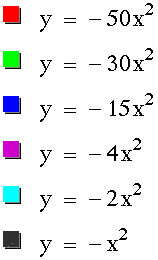
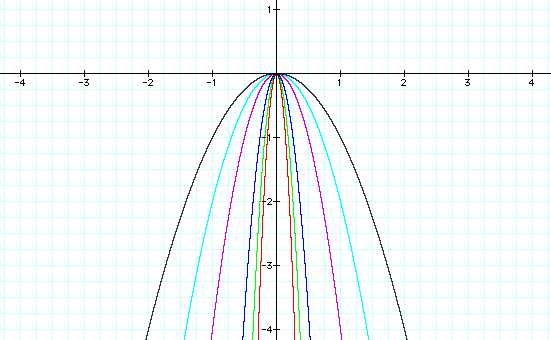It appears as though we can draw the
same conclusion when a < 0. The smaller a gets
(or the further a is from zero), the more contracted the
parabolas become.
Now, let's look at the relationship
between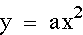 
and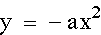 
. Looking
at the previous two graphs, we could guess that making a
negative simply reflects the parabola about the x-axis. Let's
investigate this a bit further.
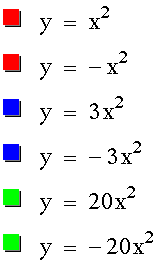
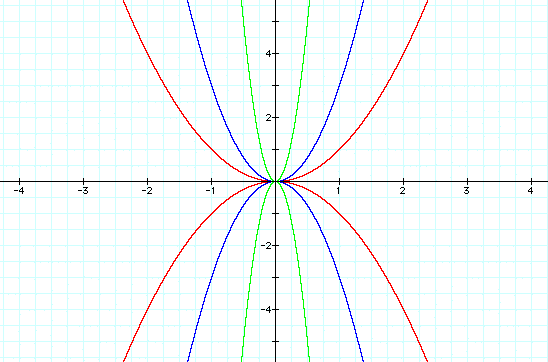Well, it looks as though our conjecture
was true!
From these graphs, we can see that
the parabolas open up when a > 0.
They open down when a < 0.
But, what happens if -1 < a
< 1 ? Let's look at a few of those.
First, we'll look at -1 < a <
0.
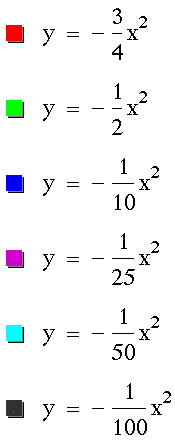
WOW! If we look at this graph on the
same scale as the others, many of the parabolas are too wide for
us to see. So, let's change the scale of the graph and get a better
look at them.
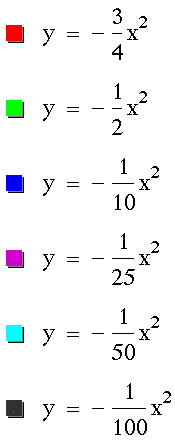
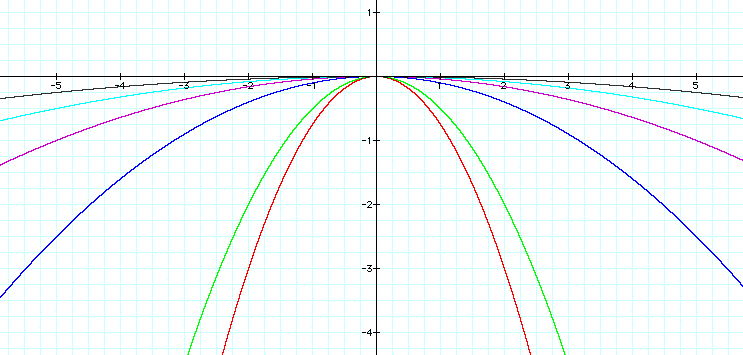
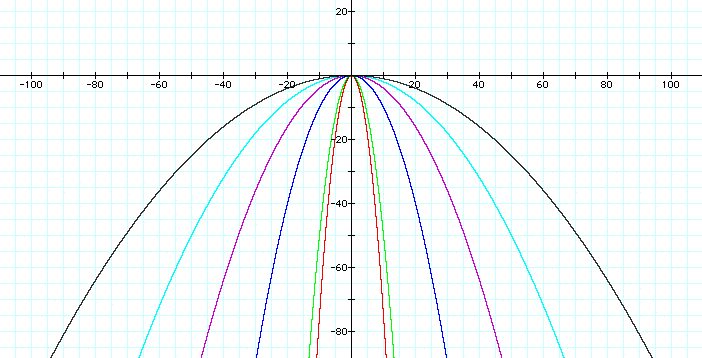That's better. Now we can see just
how wide the parabolas really are. It appears that when
-1 < a < 0, the parabolas
expand as a gets closer to zero.
Now, let's look at 0 < a < 1.
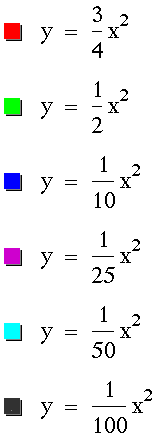
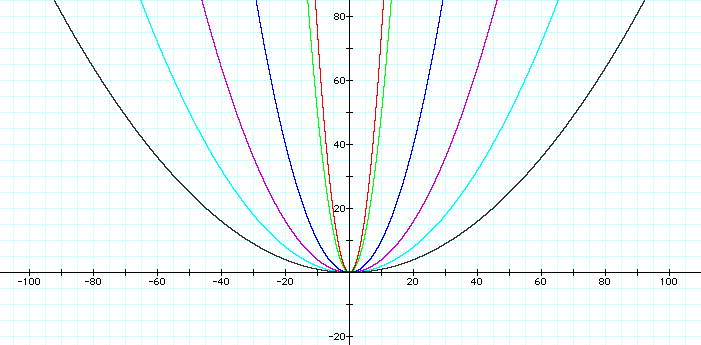Well, it looks like the same thing
is true for 0 < a < 1. The parabolas expand as a
gets closer to zero.
We can explore a bit further with a
movie that lets a vary between
-5 and 5.
Let's summarize what we've found.
When working with the graph of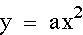 
:
1. If a > 0, then the parabola will
open up. If a < 0, the parabola will open down.
2. The further a is from zero, the more
contracted the parabola will become; OR, the closer a is
to zero, the more expanded the parabola will become.
Return
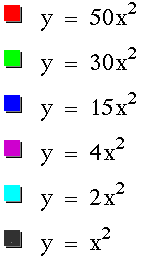
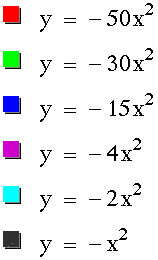
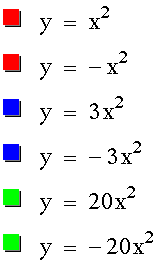
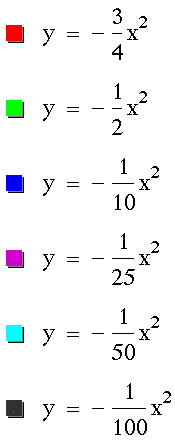
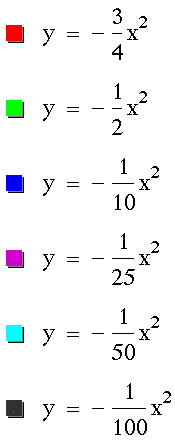
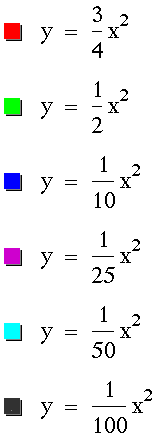