It has now become a rather standard exercise, with available technology, to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held constant. From these graphs discussion of the patterns for the roots of
can be followed.
For a different approach to this topic, we are going to examine several graphs in the xb plane.
Consider the equation
Now graph this relation in the xb
plane. We get the following graph.
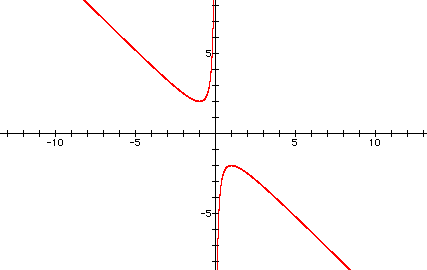
If we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
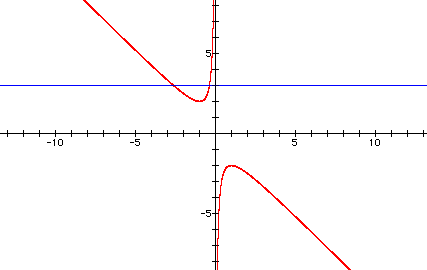
For each value of b we select, we get
a horizontal line. It is clear on a single graph that we get two
negative real roots of the original equation when b >
2, one negative real root when b = 2, no real roots for
-2 < b < 2, One positive real root when b
= -2, and two positive real roots when b < -2.
Consider the case when c = - 1 rather than + 1. We get
the following graph.
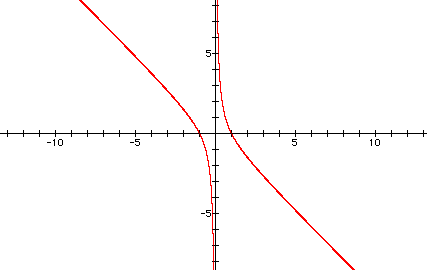
Choosing an arbitrary value for b, say b = 6, and overlay this equation on the graph we add a line parallel to the x-axis. It will intersect the curve in the xb plane and the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
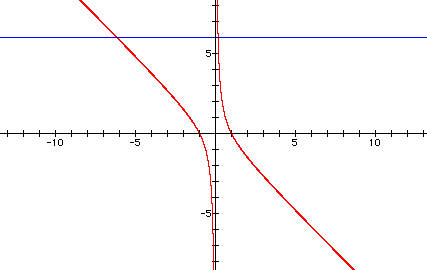
For each value of b we select, we get
a horizontal line. It is clear on a single graph that we get two
real roots of the original equation - one negative and one positive
- for any value of b we choose.
How does a affect the situation in the xb plane? The following is a graph of
with a = 0.
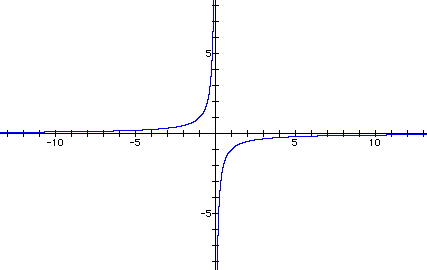
Here is a graph of
with a = 0.
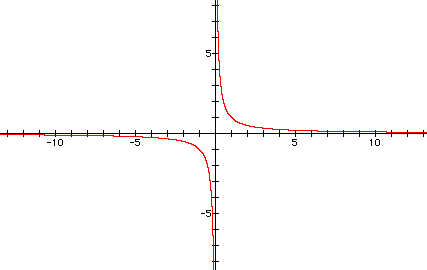
As you can see, the graphs are reflections across the y-axis.
Click here to see a movie of both of these graphs as a varies between -10 and 10.
As you can see, the value of a changes the width of the graphs. However, neither of the graphs ever cross over the y-axis. How does the value of a change the roots of the equation?
When a > 0,
has either two positive real roots when
, two negative real roots when
,
one real root when
, or no real roots
when
.
And,
has two real roots - one positive and one negative for every value of b.
When a < 0, the characteristics are flip-flopped - with the graph of
having two real roots for every value of b and the graph of
having either two positive real roots, two negative real roots, one real root, or no real roots.
And so you see, exploring the graphs of quadratic equations in the xb plane can be very informative and enlightening for students of all ages.