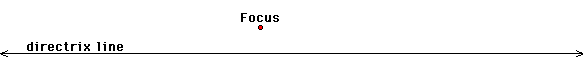Constructing Conic Sections

by: Lauren Wright

Conic sections are formed by the intersection of parallel planes and a double cone - forming ellipses, parabolas, and hyperbolas, respectively.

PARABOLAS

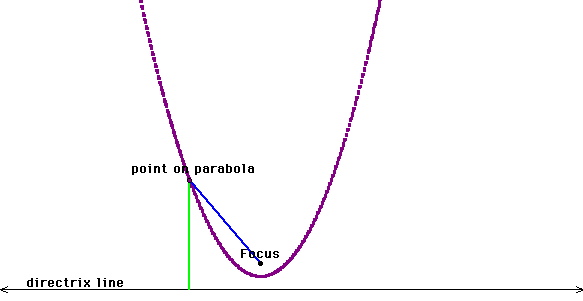
A parabola can be defined as the set of points equidistant from a line, called the directrix, and a fixed point, called the focus. In other words, for any point on a parabola, the length of the green line is equal to the length of the blue line.

We are going to construct a parabola using Geometer's Sketchpad. For our construction, we will assume that the focus does not lie on the directrix line.

1. We will begin with our directrix line and focus.

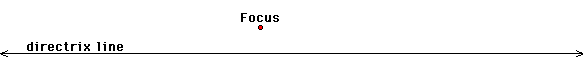2. Next, we will make a movable point on the directrix line to help us trace the path of our parabola.

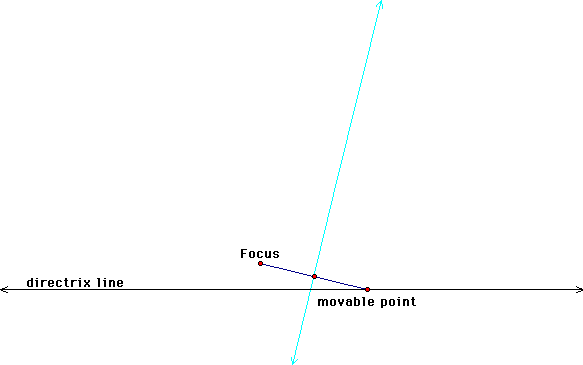
3. In order to find a point that is equidistant from the movable point and the focus, we will find the midpoint of the segment that connects them.

4. Using that midpoint, we will draw a perpendicular bisector through the segment from the movable point to the focus. This perpendicular bisector will represent one of the tangent lines to the graph of the parabola.

5. With this one tangent line, we can construct the set of all of the tangent lines to the parabola by simply moving the movable point along the directrix and tracing our tangent line.

6. With this set of tangent lines, how can we find the points that actually lie on the parabola?

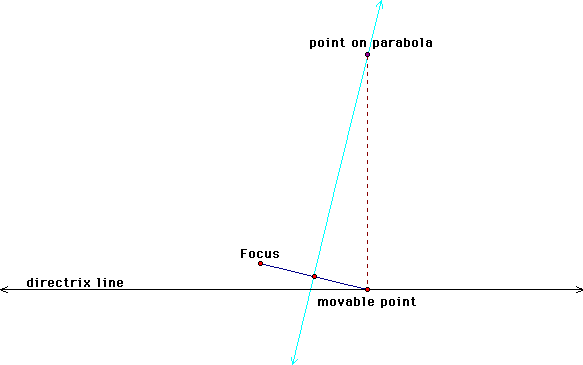
For that, we will have to remember that every point on a parabola is equidistant from the directrix and the focus. The distance from a point to a line is measured by drawing the perpendicular through the point to the line. So, if we draw a perpendicular through the movable point to intersect our original tangent line, the intersection will give us one point that lies on the parabola.

7. With this one point on the parabola, we can construct the set of all of points by simply moving the movable point along the directrix and tracing our point on the parabola.

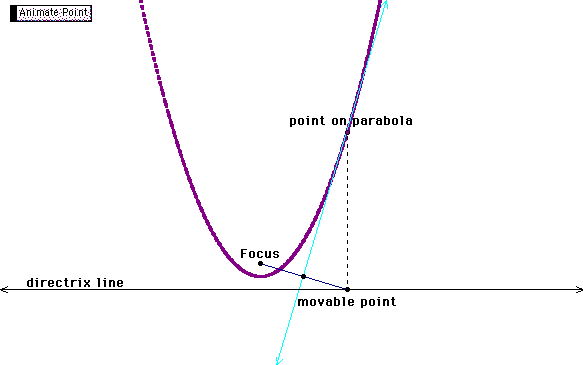And, here is our parabola! To investigate this construction yourself, click here.

ELLIPSES

An ellipse can be defined as the set of all points whose sum of its distance from two foci is a constant.

We are going to construct an ellipse using Geometer's Sketchpad. This construction will be much like the construction for the parabola. Only this time, we will let a circle act as our "directrix." For this construction, we will assume that the focus lies inside the circle.

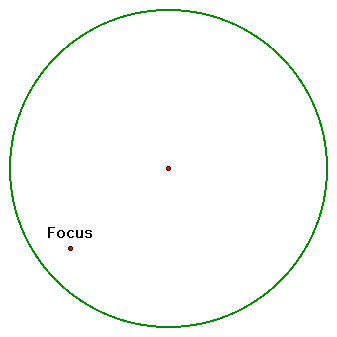
1. We will begin with our "directrix" circle and a focus.

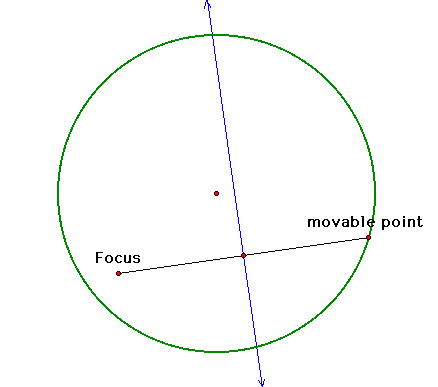
2. Following the same procedure as the parabola construction, we will construct a movable point on the circle, a segment from the movable point to the focus, and the perpendicular bisector of that segment.

3. Once again, this perpendicular bisector is one of the tangent lines to the ellipse. We can construct the set of all tangent lines by moving the movable point around the circle and tracing the tangent line.

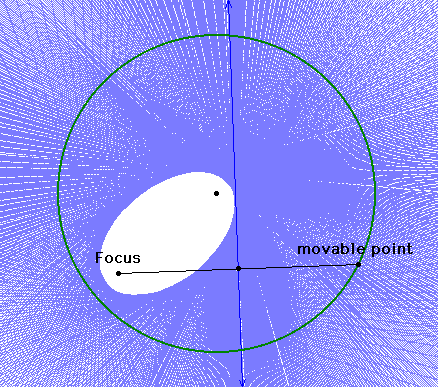4. It is interesting to note that our two foci turn out to be the original focus and the center of the circle. Is this true for any focus inside the circle? Let's find out.

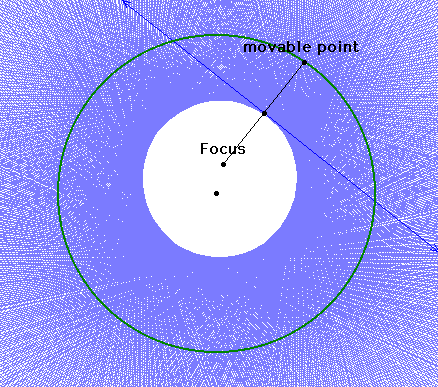5. It looks the two foci will always be the original focus and the center of the circle. Why does this ellipse appear to be more circular-shaped than our previous one?

It's because the focus we chose is closer to the center of the circle!

To investigate this construction yourself, click here.

HYPERBOLAS

A hyperbola can be defined as the set of all points the difference of whose distances from two foci is a constant.

We will construct a hyperbola in Geometer's Sketchpad using the same methods we used for the ellipse construction. The only difference will be that we choose our focus to be outside the circle.

1. We will begin this time with our "directrix" circle, our focus, and our tangent line already constructed.

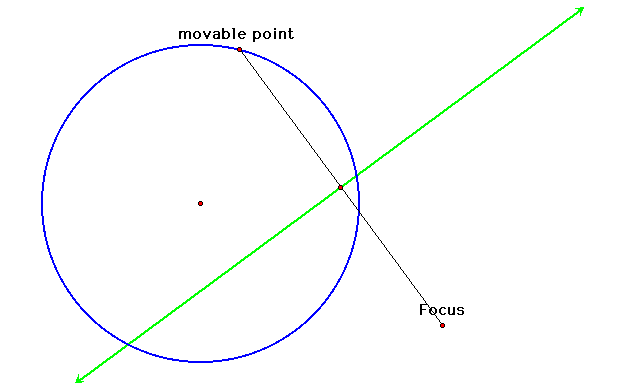2. In the same manner as before, we will trace the tangent line while moving the movable point around the circle.

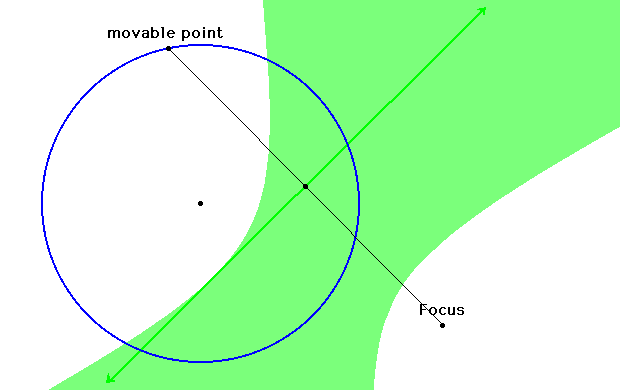3. Here we can see that our tangent lines form the shape of a hyperbola. Similar to the ellipse, the two foci will be the original focus and the center of the circle.

Ton investigate this construction yourself, click here.

This concludes our investigations of conics!

 

 

 

Return