investigations of tangent circles

Investigations with Tangent Circles

something I discovered

by: Lauren Wright

In this investigation, we take a look at some properties of tangent circles. In order to explore these properties, we will need to work with two main constructions. Given two circles and a point, P, on one of the circles, construct a circle tangent to the two circles with one point of tangency being P.

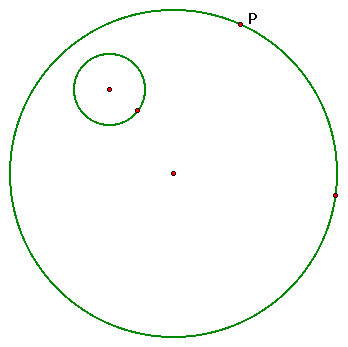One possible construction would make the smaller circle external to the tangent circle.

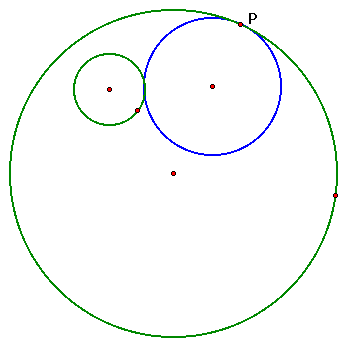Another possible construction would make the smaller circle internal to the tangent circle.

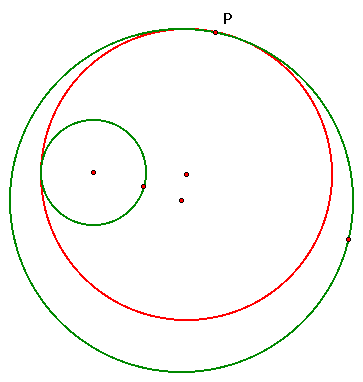These are the two possible tangent circles for this construction. To see the motivation behind these constructions, click here to go to Dr. Jim Wilson's Assignment 7 Page.

OR, click here to download a file with the two constructions and a script tool in it.

Now, let's take a look at the loci of the centers of the tangent circles.

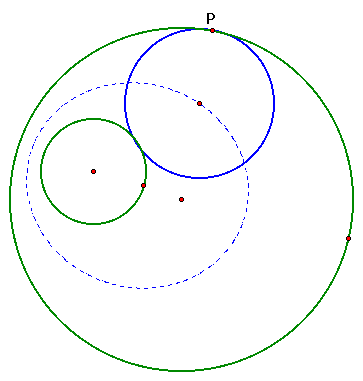
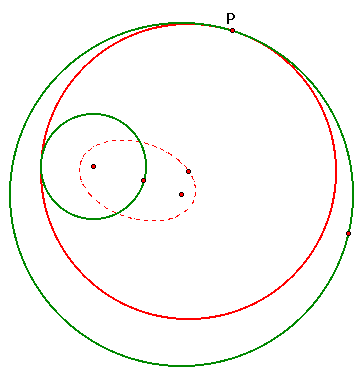The loci of the centers of the tangent circles take the shape of an ellipse. An ellipse is the loci of all points whose sum of the distances from two foci is a constant. In this case, the two foci would be the centers of the original circles.

What does THAT mean? It means that no matter where the center of the tangent circle is, the sum of its distances from the two foci will remain constant. Click here to explore this relationship by moving the point of tangency, P, around the original circle.

Now, the obvious question is, will the loci of the centers of the tangent circles always form an ellipse? Let's take a look.

CASE 1: What happens if the two original circles intersect?

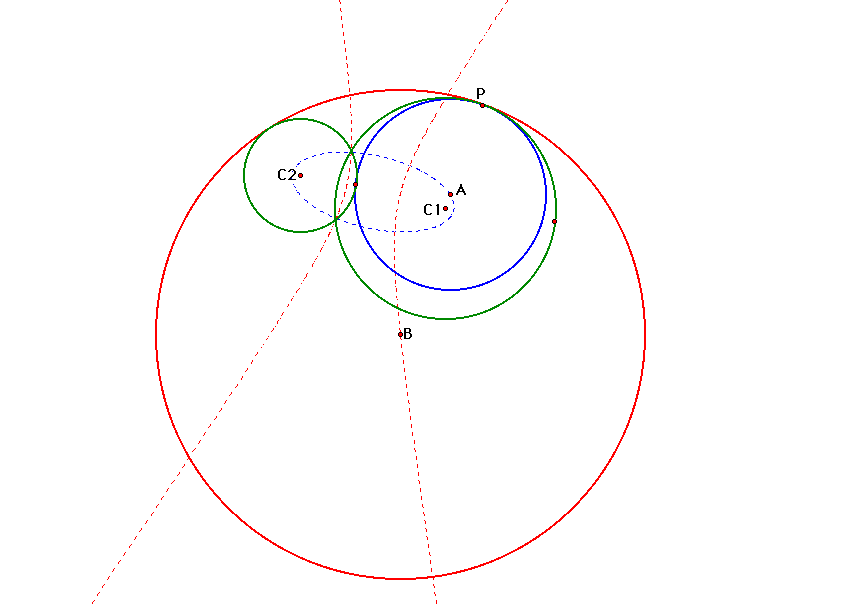This time, the loci of the blue circle is an ellipse. BUT, the loci of the red circle is a hyperbola. The foci are still the centers of the two original circles.

What is the relationship of the foci with a hyperbola? Well, a hyperbola is the loci of all points whose difference of the distances from the two loci is a constant. Click here to explore this relationship by moving the point of tangency, P, around the original circle.

CASE 2: What happens if the two original circles are disjoint?

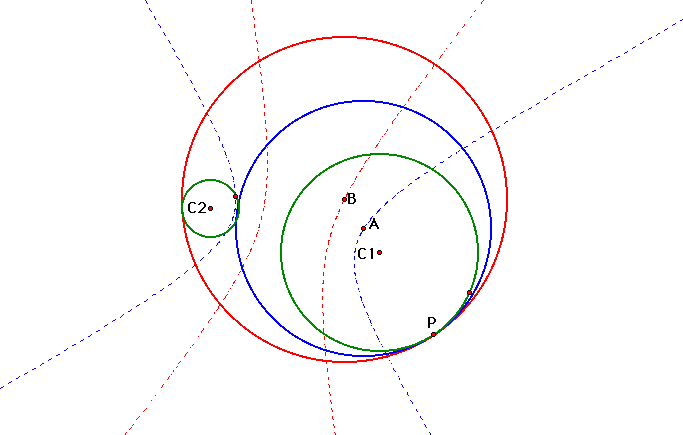Here we see that the loci of the centers of the tangent circles are both hyperbolas. Click here to explore this relationship.

After exploring the paths of these loci, I found that they had formed two of the conic sections - the ellipse and the hyperbola. So, my next question was, "Can I change the original circles so that the loci form the other significant conic section, the parabola?"

To do this, I manipulated the sketch above until the loci formed a parabola on the screen. When the parabolas appeared on the screen, the two original circles were disjoint and I had made one of them really large.

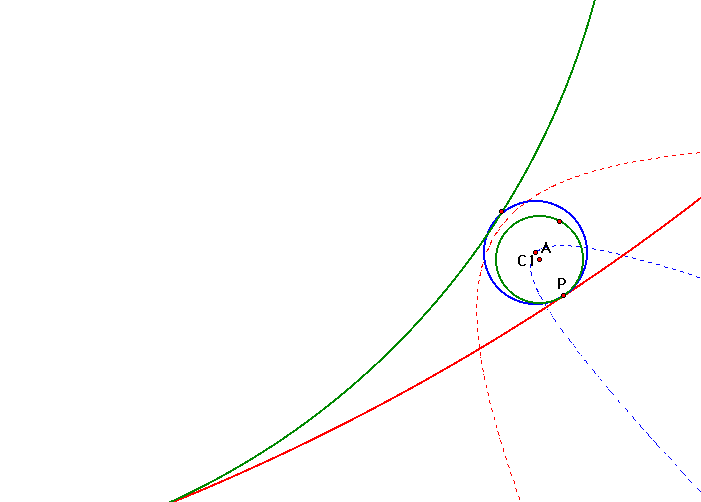
In this picture, you cannot even see the center of the circle that I made large. The large circle appears to be approaching a line as I drag the center further and further.

Recall that the foci of the two hyperbolas are the centers of the two original circles. My conclusion is that as one foci approaches infinity, the loci will approach a parabola. In other words, the loci forming a parabola is a limiting case.

Return