Investigations with the Pedal Point, the Pedal Triangle, and the Incircle

by: Lauren Wright

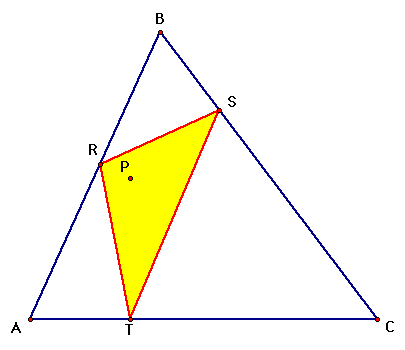
In this investigation, we begin with any triangle ABC. Then if P is any point in the plane then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points, R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

For example:

Click here to explore this construction yourself.
In this exploration, we construct the incircle of triangle ABC and then choose P to be a point on the incircle.

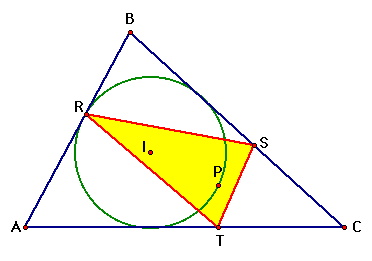Then we construct the midpoints of the sides of the pedal triangle RST.

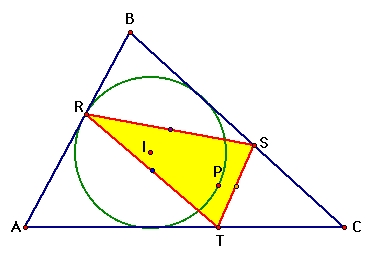Next, we animate the pedal point P about the incircle of ABC and trace the loci of the midpoints of the sides.

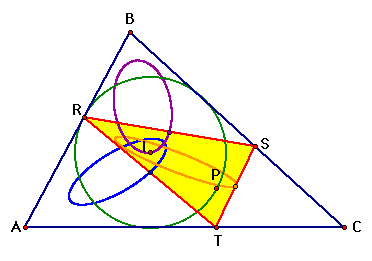And we see that the loci of the midpoints of the sides of the pedal triangle form ellipses as P is animated along the incircle.

Click here to explore this construction yourself.

Now, let's look at what happens when ABC is a right triangle.

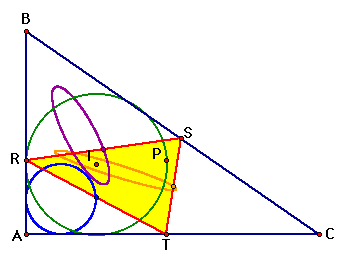Here we see something interesting happening - the blue locus appears to form a perfect circle that is tangent to ABC at two points.

Click here to explore this construction yourself.

Now the question becomes, why does this happen?

We begin by drawing in some auxiliary lines.

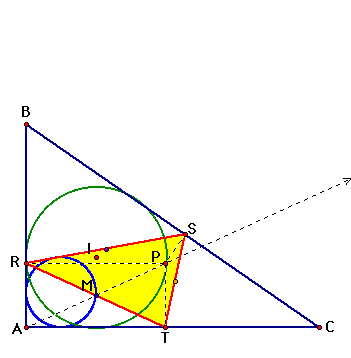Notice here that ray AP always goes through that blue midpoint, which we have now labeled M.

Now, let's take a look at that right triangle that has been formed, triangle APT.

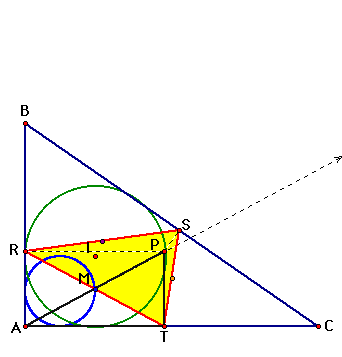It appears that M is the midpoint of the hypotenuse of triangle APT - we can verify this with GSP.

Or, we can look at rectangle ARPT. RT and AP are diagonals of this rectangle and diagonals of a rectangle always bisect each other. So, M must be the midpoint of AP.

Now, we can make a triangle similar to APT by dropping a perpendicular from M to segment AT. These two triangles will be similar by angle-angle similarity.

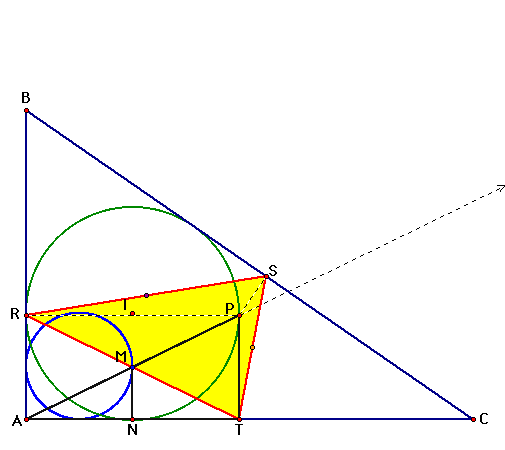Since triangle AMN is similar to triangle APT, as point P travels around the incircle, M will also form a perfect circle - a circle that will in fact, have half the radius of the incircle.

 

Return