

Contrary to popular beliefs math and math teachers are not all 'mean'. For this assignment, I am going to explore the mean components of math and hopefully clear up some of my own misconceptions.
"We shall therefore borrow all our Rules for the Finishing our Proportions, from the Musicians, who are the greatest Masters of this Sort of Numbers, and from those Things wherein Nature shows herself most excellent and compleat."
Leon Battista Alberti (1407-1472)
There are several different types of means in mahematics. I will only look at a few, but I would like to begin with a clarification of the definition of a mean. A mean is an intermediate value between two other values as determined by a specific formula or set of conditions. A mean is a propotional value. It holds a relationship between two extreme values. Means have long been studied by mathematicians, architects, musicians, and philosophers. The majority of means found in mathematics are much more complex than the 'average' of a set of numbers.
Arithmetic Mean
The most commonly familiar mean is the arithmetic mean. We are familiar with how to average grades. In mathematics, the arithmetic mean is defined as
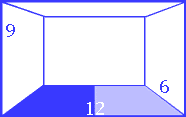
for all a's being real numbers. Palladio uses the representation of a room with measurements 12' long and 6' wide. He concludes that the third side (height) is 9' because 12 exceeds 9 by 3 and 9 exceeds 6 by the same amount of 3.
Geometric Mean
The geometric mean is defined for all a's being real and positive numbers as
Palladio describes GM as a proportion of the sides. In this example, you multiply the lesser extreme by the greater extreme and take the square root.

Here is a GSP construsion of a triangle with the arithmetic mean and geometric mean as two of its sides.
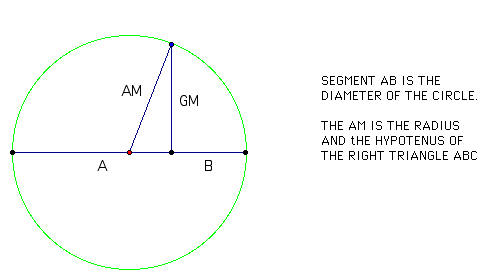
From the geometric aspect, AM has to be greater than the GM because of the definition on hypotenuse.
Harmonic Mean
The harmonic mean is defined for a being positive numbers as
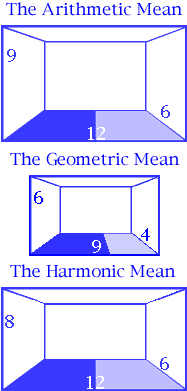
Palladio compared Arithmetic, Geometric, and Harmonic Means with this picture.
Click here for a problem using Harmonic Mean.
Arithmetic-Geometric-Harmonic Mean Inequality
Each of these means lie between a maximium and a minimum value. In comparison to each other, the inequality would look like the following:
This inequality
can be verified for all positive numbers x and y.
Here is a GSP construction of a trapezoid that represents the arithmetic mean, geometric mean, and harmonic mean.

Noe let us look at the arithmetic-geometric mean inequality.
We can verify this for all positive x's and y's. The squares can then be used to obtain.
By substituton, this equation is obtained.
This equality is equivalent to
Therefore,
Since a and b are positive, this equation is true and the arithmetic-geometric mean inequality is