


Click HERE for background information on Ptolemy.
Ptolemy's theorem is
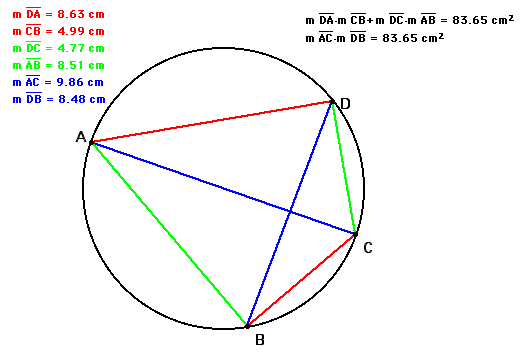
Ptolemy's Theorem provides a way to prove trigonometric identities. It implies the Pythagorean Theorem. The Pyhthagorean Theorem is utilized once the qudrilateral becomes a rectangle. Since three points determine a circle, the forth point of the qudrilateral becomes the constraint and determines whether the quadrilateral is cyclic or not. Once the constraint is met then the product of the diagonals of the cyclic quadrilateral equals the sum of the products of the opposite sides of the cyclic quadrilateral.
Proof of Ptolemy's Theorem
When the quadrilateral is not cyclic then Ptolemy's Theorem becomes an inequality.