5.1 Perimeter and Area

Geometry

Holt, Rinehart, and Winston

 

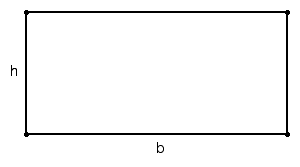
Objective:

* Identify and use the Area of a Rectangle and the Sums of Area Postulates

* Solve problems involving fixed perimeters and fixed areas.

 

Perimeter:

Definition: The perimeter of a closed plane figure is the distance around the figure.

P= a +b

Primeter of an irregular figure can be approximated by using a polygon.

 

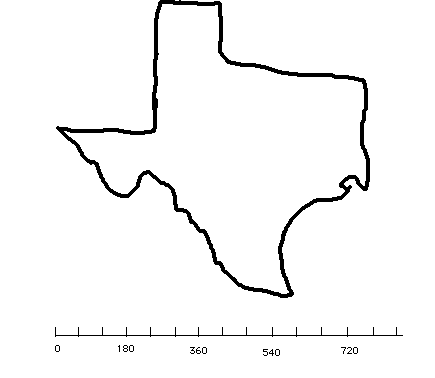
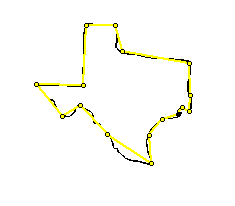
Now the figure has 14 sides and the length can be taken for each side and added together to approximate the perimeter of Texas.

Area:

Definition: The area of a closed plane figure is the number of non-overlapping squares of a given size that will exactly cover the interior of the figure.

A = b * h

 

Example:

h = 2 squares and b = 4 squares

A= 2 squares *4 squares = 8 squares

 

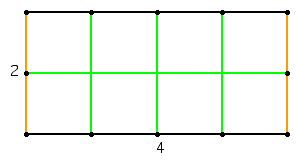
To find nonrectangular shapes use the Postulate for The Sum of Areas. The Postulate for the Sum of Areas is if the figure is composed of non-overlapping regions A and B, then the area of the figure is the sum of the areas of regions A and B.

Example: Find the area of the figure ABCD without the figure EFGH.

 

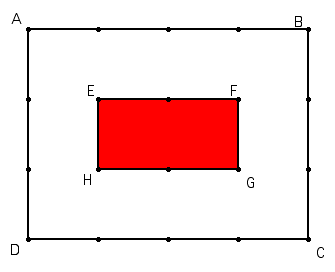
You can find the area by dividing the section into rectangles and adding the areas together.

 

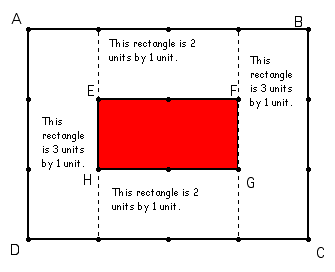
The area is the addition of each section (3*1) + (2*1) + (3*1) + (2*1) = 10. You can also obtain the area by finding the area of the larger rectangle and subtracting the area of the smaller (4*3) - (2*1) = 10.

 

Fixed Perimeter/Maximum Area:

Now you can use the information above to answer questions to problems such as if given a fixed perimeter what will be the maximum area you can have. Let me use a perimeter of 24 as an example.

A = b*h and P = 2b + 2h

if P = 24 then 24 = 2b + 2h and 12 = b + h

solve for h = 12 - b

substitute h into area and you get

A = b(12 - b) or A = 12b - b^2

Now graph the equation for area

 

As you can see maximum area is obtained when x and y are 6. Therefore maximum area with a fixed perimeter is obtained when the region is a square.

 

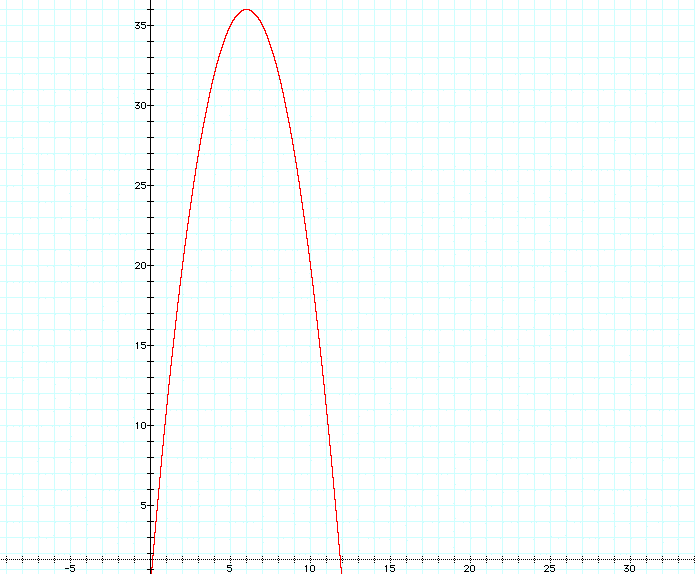
Fixed Area/Minimum Perimeter:

Now let us see if a fixed area produces the same result. Given an area of 3600 what is the minimum perimeter you would need?

A = b*h and P = 2b + 2h

A = 3600 = b*h

so h = 3600 / b

P = 2b + 2h so P = 2b + 2(3600 / b)

Now graph it.

 

Minimum perimeter is obtained when the length and width are equaled which would give you a square. When graphing this a hyperbola is obtained, but since lengths can not be negative that side of the graph can be overlooked.

 

 

 

Return to Instructional Unit