Objectives:

* Develop formulas for the areas of triangles, parallelograms, and trapezoids.

* Solve problems by utilizing formulas for the areas of triangles, parallelograms, and trapezoids.

Triangles:

I. Parts of a triangle -

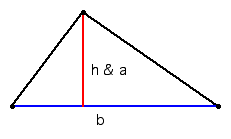
Base (b): any side of the triangle can be called a base

Altitude (a): the perpendicular segment from a vertex to a line containing the base of the triangle

Height (h): the length of the altitude

Note: For any side you choose as the base of the triangle, there is a corresponding altitude.

II. Deriving the formula of the area of a triangle -

1. Start by drawing a rectangle and calculate the area, because you already know the formula for area of a rectangle.

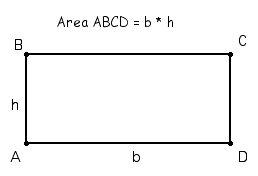
2. Construct a diagonal to form two right triangles. From the previous study of special quadrilaterals, students should be aware that a diagonal of a rectangle cuts the rectangle into two equal areas.

 

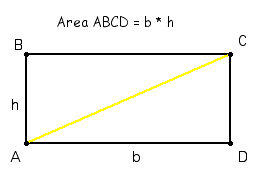
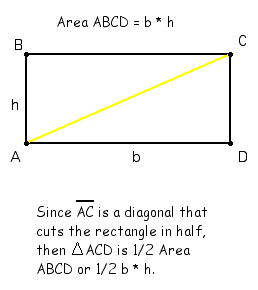
3. Derive the formula for a triangle using the area of a rectangle.

 

4. To derive the area for any triangle. Construct a scalene triangle in a rectangle. Is the altitude parallel to the sides of the rectangle.?

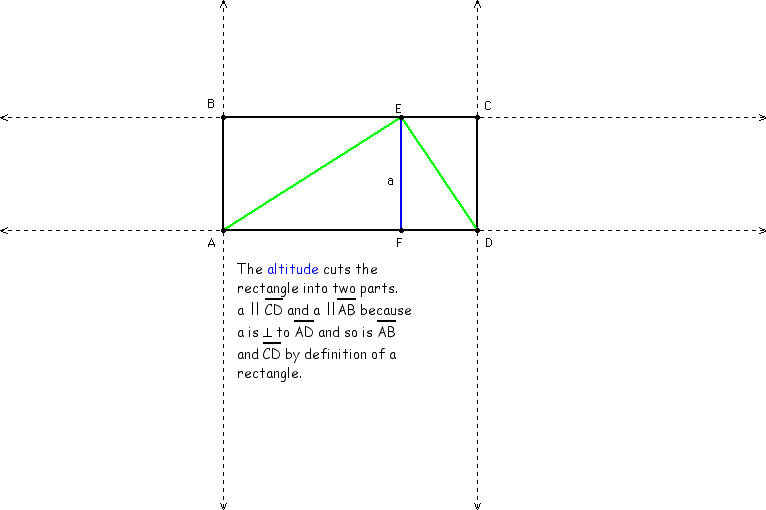
The altitude cuts the rectangle into two smaller rectangles that contain two right triangels each. We can use the previous knowledge of how to find the area of a right triangle to determine the area of a scalene triangle.

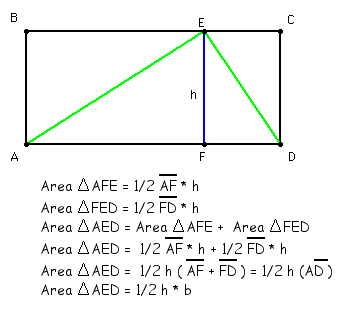
Click here for a GSP construction to see if this formula holds for all triangles.

 

III. Area of a triangle -

The area of a triangle with a base b and height h is one-half the produst of base times height. A = 1/2 b * h

 

Parallelograms:

I. Parts of a parallelograms -

 

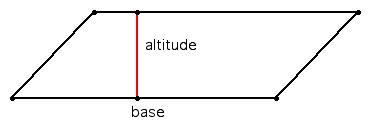
Base (b): any side of the parallelogram

Altitude (a): the perpendicular segment from a line containing the base to a line containing the opposite side

Height (h): the length of the altitude

II. Derive the formula of a parallelogram -

1. Draw a parallelogram

2. Cut with an altitude which will cut the parallelogram into two parts

3. Take the two parts and put them back together with the two sides with angles not a right angle overlapping.

4. This constructs a rectangle by definition of a parallelogram. From previous knowledge, students are aware that the area of a rectangle is A = b * h.

 

Trapezoids:

I. Parts of a trapezoid -

Base (b): is one side of the set of parallel sides

Legs (l): the set of nonparallel sides

Altitude (a): the perpendicular segment from one base to the other

Height (h): length of the altitude

 

II. Derive the formula for the area of a trapezoid -

1. Cut the trapezoid into shapes that we already know the formula for area. Start by constructing two altitudes from points A and B. These gets a shape with two traingles and a rectangle.

2. Add the areas together to form the formula of the area of a trapezoid.

Return to Instructional Unit