Let us review the parts of a circle.
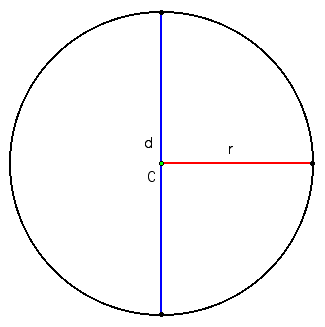
A circle is a set of points in a plane that aar eequal distance, r (radius), from a given point in the plane known as the center (C) of the circle. The distance d = 2r is known as the diameter of the circle.
Objectives:
* Identify and apply formulas for the circumference and area of a circle.
* Solve problems using the formulas for the circumference and area of a circle.
The Definition of a Circle:
Let us review the parts of a circle.
A circle is a set of points in a plane that aar eequal distance, r (radius), from a given point in the plane known as the center (C) of the circle. The distance d = 2r is known as the diameter of the circle.
Circumference of a Circle:
By the time students enter a geometry classroom, they have used circumference and area. They were given formulas and were taught to apply those formulas to a set of numbers. In this text, the students are geared to look at the circumference in relationship to "pie and area in relationship objects already studied..
Definition: The circumference of a circle is the distance around the circle. The circumference of a circle, C, with diameter, d, and radius, r, is given by:
Now look at three different circles:
On average the ratio of the three circles is
(3.13951+3.1352+3.14)/3 = 3.13824 The more circles there are the more the ratio of C/d will converge to 3.14.
Here is a brief history of Pi from Wolfram Research website.
Area of a Circle:
The area, A, of a circle with radius, r, is given by:
Return to Instructional Unit