Objectives:

* Identify and apply the Pythagorean Theorem and its converse.

* Solve problems using the Pythagorean Theorem.

 

History of the Pythagorean Theorem:

The Babylonians used the properties of right triangles way before he teacher Pythagoras was alive. The usage was discovered on a tablet known as Plimpton 322. Parts of this tablet are lost, but the part that remains clearly shows that the Babylonians knew about the Pythagorean triples. There is no direct evidence at this time that the Babylonians could prove the Pythagorean Theorem.

Click here to read more about the Pythagorean triples.

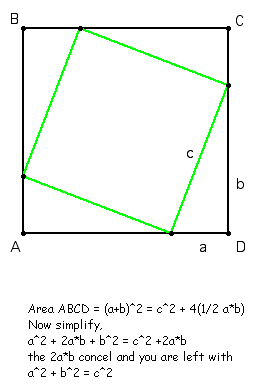
Proving the Relationship for Right Triangles:

There are many different ways to prove the Pythagorean Theorem. This example comes from an ancient Chinese source known as Chou pei suan ching diagram. Some scholars believe it dates as far back as Pythagoras. This source utilizes four congurent triangles in a square. The formulas already known can be used to develop as start to obtain the Pythagorean Theorem.

 

Click here to look at 43 different proofs of the Pythagorean Theorem. Proof #4 is used in the above example.

The Converse of the Pythagorean Theorem:

The converse of the Pythagorean Theorem is if the square of the length of one side of a triangle equals the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle. To illustrate let us look at a GSP sketch. In this sketch there is a triangle that is not right and three squares surrounding the triangle and are located at each of its sides.

 

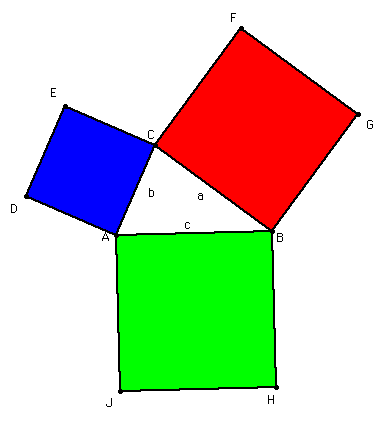
Now you can use GSP to look at the areas of the squares surrounding the triangle and the area of the triangle. What happens when angle ACB is not a right angle. Click here to explore.

Click here for a formal proof of the converse of the Pythagorean theorem.

Pythagorean Inequalities:

For triangle ABC, with c being the longest side:

* If c^2 = a^2 + b^2, then triangle ABC is a right triangle.

* If c^2 > a^2 + b^2, then triangle ABC is an obtuse triangle.

* If c^2 < a^2 + b^2, then the triangle ABC is an acute triangle.

 

 

Retrun to Instructional Unit